CF1085D Minimum Diameter Tree

给定一棵树（无环连通无向图）和一个整数 $s$。 Vanya 想要给树的所有边分配权值，使得所有权值都是非负实数，并且它们的和为 $s$。同时，他希望使树的直径尽可能小。 我们定义加权树的直径为树中某两点之间路径上所有边权之和的最大值。换句话说，加权树的直径就是树中最长简单路径的长度，其中路径的长度等于路径上所有边权之和。 请你求出 Vanya 能够得到的最小可能直径。

第一行包含两个整数 $n$ 和 $s$（$2 \leq n \leq 10^5$，$1 \leq s \leq 10^9$），分别表示树的顶点数和所有边权之和。 接下来的 $n-1$ 行，每行包含两个用空格分隔的整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq n$，$a_i \neq b_i$），表示一条无向边连接顶点 $a_i$ 和 $b_i$。 保证给定的边构成一棵树。

输出 Vanya 通过分配权值后能够得到的最小直径。 如果你的答案的绝对误差或相对误差不超过 $10^{-6}$，则视为正确。 形式化地说，设你的答案为 $a$，标准答案为 $b$，当 $\frac{|a-b|}{\max(1, b)} \leq 10^{-6}$ 时，视为正确。

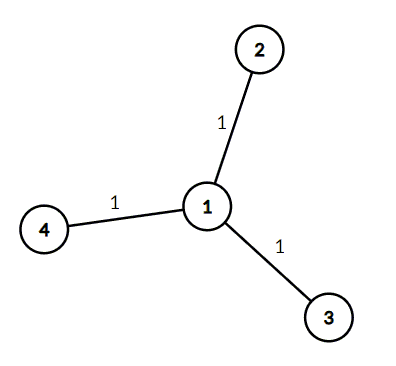
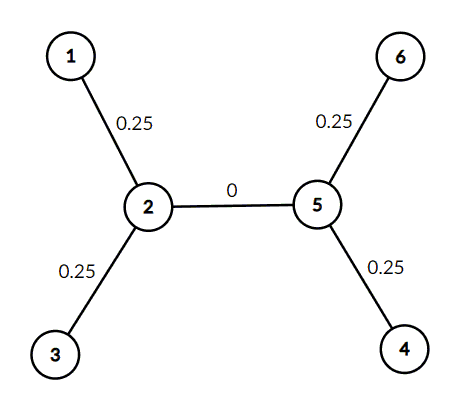
在第一个样例中，应该将权值分配如下：  可以很容易看出，这棵树的直径为 $2$。可以证明这是最小可能的直径。 在第二个样例中，应该将权值分配如下：  由 ChatGPT 4.1 翻译