CF1088F Ehab and a weird weight formula
题目描述
给定一棵包含 $n$ 个节点的树。每个节点 $u$ 有一个权值 $a_u$。保证树中只有一个节点的权值最小。对于每个节点 $u$(除了权值最小的节点),它必须有一个相邻的节点 $v$,使得 $a_v < a_u$。你需要构造一棵树,使得权值 $w$ 最小,$w$ 的计算方式如下:
- 对于每个节点 $u$,将 $deg_u \cdot a_u$ 加入 $w$($deg_u$ 表示包含节点 $u$ 的边的数量)。
- 对于每条边 $\{u,v\}$,将 $\lceil \log_2(dist(u,v)) \rceil \cdot \min(a_u, a_v)$ 加入 $w$,其中 $dist(u,v)$ 表示在给定树中从 $u$ 到 $v$ 的路径上的边数。
输入格式
第一行包含一个整数 $n$,表示树的节点数,$2 \le n \le 5 \times 10^5$。
第二行包含 $n$ 个用空格分隔的整数 $a_1, a_2, \ldots, a_n$,表示每个节点的权值,$1 \le a_i \le 10^9$。
接下来的 $n-1$ 行,每行包含两个用空格分隔的整数 $u$ 和 $v$,表示节点 $u$ 和节点 $v$ 之间有一条边,$1 \le u,v \le n$。
输出格式
输出一个整数,表示 $w$ 的最小可能值。
说明/提示
在第一个样例中,原树本身就能使 $w$ 最小。
在第二个样例中,最优的树结构如下:
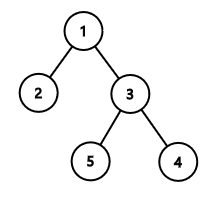
由 ChatGPT 4.1 翻译