CF1088F Ehab and a weird weight formula
Description
You're given a tree consisting of $ n $ nodes. Every node $ u $ has a weight $ a_u $ . It is guaranteed that there is only one node with minimum weight in the tree. For every node $ u $ (except for the node with the minimum weight), it must have a neighbor $ v $ such that $ a_v
Input Format
The first line contains the integer $ n $ $ (2 \le n \le 5 \cdot 10^5) $ , the number of nodes in the tree.
The second line contains $ n $ space-separated integers $ a_1, a_2, \ldots, a_n $ $ (1 \le a_i \le 10^9) $ , the weights of the nodes.
The next $ n-1 $ lines, each contains 2 space-separated integers $ u $ and $ v $ $ (1 \le u,v \le n) $ which means there's an edge between $ u $ and $ v $ .
Output Format
Output one integer, the minimum possible value for $ w $ .
Explanation/Hint
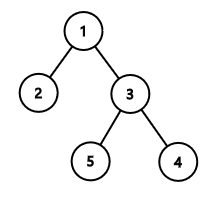
In the first sample, the tree itself minimizes the value of $ w $ .
In the second sample, the optimal tree is: