CF1098C Construct a tree

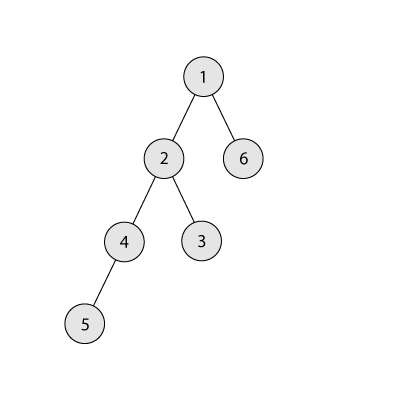
Misha 漫步在雪地森林中，被树木深深吸引，决定画一棵属于自己的树！ Misha 想要构造一棵有 $n$ 个结点的有根树，结点编号从 $1$ 到 $n$，其中根结点编号为 $1$。每个其他结点都有一个父结点 $p_i$，$i$ 被称为结点 $p_i$ 的子结点。若从 $u$ 出发，沿着父结点链（$u$，$p_u$，$p_{p_u}$，……）能够到达 $v$，则称结点 $u$ 属于结点 $v$ 的子树。显然，$v$ 也属于自己的子树，子树中结点的数量称为子树的大小。Misha 只对所有结点都属于结点 $1$ 的子树的树感兴趣。 下图是一棵有 $6$ 个结点的树。结点 $2$ 的子树包含结点 $2$、$3$、$4$、$5$，因此其子树大小为 $4$。  树的分支系数定义为任意结点的最大子结点数。例如，上图中树的分支系数为 $2$。你的任务是构造一棵有 $n$ 个结点的树，使得所有结点的子树大小之和等于 $s$，并且分支系数尽可能小。

输入仅一行，包含两个整数 $n$ 和 $s$，分别表示树的结点数和期望的所有子树大小之和（$2 \le n \le 10^5$，$1 \le s \le 10^{10}$）。

如果不存在满足条件的树，输出“No”。否则，第一行输出“Yes”，第二行输出 $p_2, p_3, \ldots, p_n$，其中 $p_i$ 表示结点 $i$ 的父结点编号。

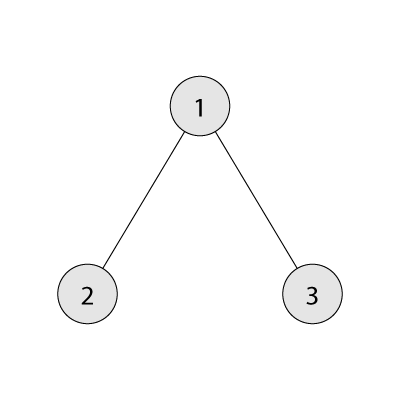
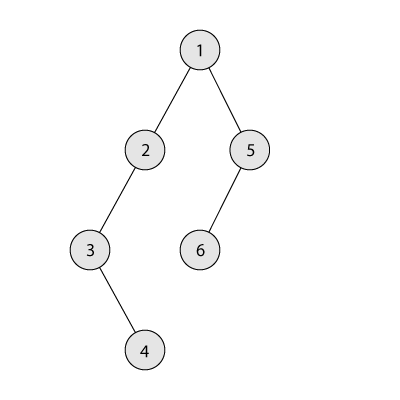
下面是第一个样例的其中一种可能解。所有子树大小之和为 $3 + 1 + 1 = 5$，分支系数为 $2$。  下面是第三个样例的其中一种可能解。所有子树大小之和为 $6 + 3 + 2 + 1 + 2 + 1 = 15$，分支系数为 $2$。  由 ChatGPT 4.1 翻译