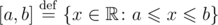CF109E Lucky Interval

Petya loves lucky numbers. We all know that lucky numbers are the positive integers whose decimal representations contain only the lucky digits 4 and 7. For example, numbers 47, 744, 4 are lucky and 5, 17, 467 are not. One day Petya came across an interval of numbers $ [a,a+l-1] $ . Let $ F(x) $ be the number of lucky digits of number $ x $ . Find the minimum $ b $ $ (a<b) $ such, that $ F(a) $ = $ F(b) $ , $ F(a+1) $ = $ F(b+1) $ , ..., $ F(a+l-1) $ = $ F(b+l-1) $ .

The single line contains two integers $ a $ and $ l $ ( $ 1

On the single line print number $ b $ — the answer to the problem.

Consider that $ [a,b] $ denotes an interval of integers; this interval includes the boundaries. That is,