CF1108F MST Unification

给定一个无向带权连通图，包含 $n$ 个顶点和 $m$ 条边，图中没有自环和重边。 第 $i$ 条边为 $e_i = (u_i, v_i, w_i)$，表示顶点 $u_i$ 和 $v_i$ 之间有一条权值为 $w_i$ 的边（$1 \le w_i$）。该图是连通的，即对于任意一对顶点，都存在仅由图中边组成的路径将它们连接起来。 最小生成树（MST）是指在所有能够连接所有顶点的边的子集中，总权值最小的那一个（总权值为所选边权值之和）。 你可以对给定的图进行如下操作：将某条边的权值增加 $1$。每条边可以被增加多次（也可以不增加）。 假设初始最小生成树的权值为 $k$。你的任务是通过最少次数的操作，使得最终图的最小生成树权值仍为 $k$，但最小生成树是唯一的（即只有一种方式选择最小生成树）。 请计算完成上述目标所需的最少操作次数。

输入的第一行包含两个整数 $n$ 和 $m$（$1 \le n \le 2 \cdot 10^5,\, n - 1 \le m \le 2 \cdot 10^5$），分别表示初始图的顶点数和边数。 接下来的 $m$ 行，每行包含三个整数，描述一条边 $e_i$。第 $i$ 行为 $u_i, v_i, w_i$（$1 \le u_i, v_i \le n,\, u_i \ne v_i,\, 1 \le w_i \le 10^9$），表示顶点 $u_i$ 和 $v_i$ 之间有一条权值为 $w_i$ 的边。 保证图中没有自环和重边（即对于每个 $i$，$u_i \ne v_i$，且对于每对无序顶点对 $(u, v)$，最多只有一条边连接它们）。保证给定的图是连通的。

输出一个整数，表示使最小生成树唯一且权值不变所需的最少操作次数。

第一个样例对应的图如下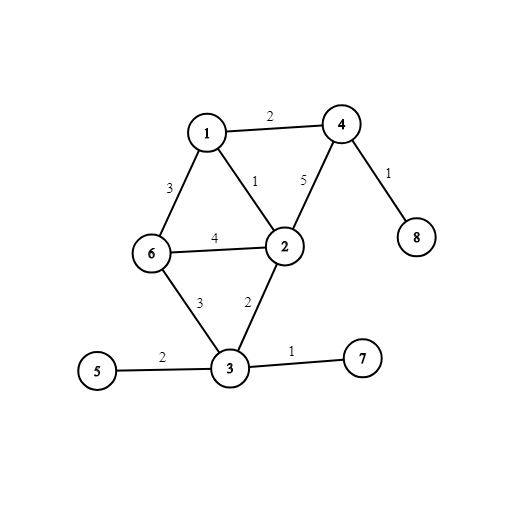： 你可以将边 $(1, 6)$ 或 $(6, 3)$ 的权值增加 $1$，即可使最小生成树唯一。 最后一个样例对应的图如下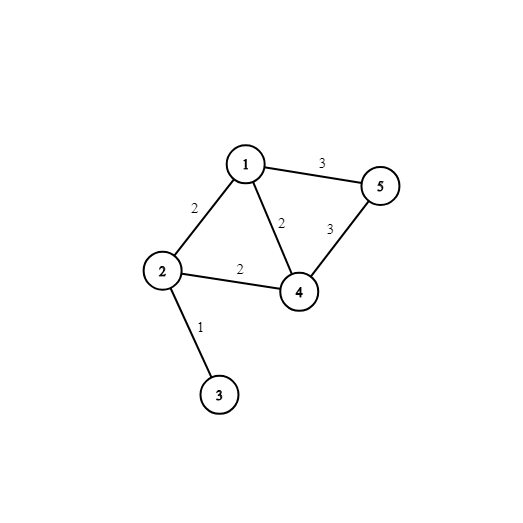： 你可以将边 $(1, 5)$ 和 $(2, 4)$ 的权值各增加 $1$，即可使最小生成树唯一。 由 ChatGPT 4.1 翻译