CF1109D Sasha and Interesting Fact from Graph Theory

有一次，在上课时，Sasha 感到无聊，决定和朋友们聊天。突然，他看到了 Kefa。关于 Kefa 的话题可以聊个没完没了，所以我们就不展开了。话题转到了图论。Kefa 承诺，如果 Sasha 帮他计算出美丽树的数量，他就会告诉 Sasha 一个有趣的图论事实。 在本题中，一棵树是一个带权连通图，由 $n$ 个顶点和 $n-1$ 条边组成，边的权值是 $1$ 到 $m$ 之间的整数。Kefa 这样定义一棵树的美丽：他在树中找到他最喜欢的两个顶点——编号为 $a$ 和 $b$ 的顶点，并计算它们之间的距离。顶点 $x$ 和 $y$ 之间的距离是从 $x$ 到 $y$ 的简单路径上所有边的权值之和。如果顶点 $a$ 和 $b$ 之间的距离等于 $m$，那么这棵树就是美丽的。 Sasha 喜欢图论，更喜欢有趣的事实，所以他同意帮助 Kefa。幸运的是，Sasha 认识你——Byteland 最棒的程序员。请你帮助 Sasha 计算美丽树的数量。两棵树被认为是不同的，如果存在一条边只出现在其中一棵树中，或者同一条边的权值不同。 Kefa 提醒 Sasha，美丽树的数量可能非常多，因此只需要输出答案对 $10^9+7$ 取模后的结果。

第一行包含四个整数 $n$、$m$、$a$、$b$（$2 \le n \le 10^6$，$1 \le m \le 10^6$，$1 \le a, b \le n$，$a \neq b$）——树的顶点数、边权的最大值，以及 Kefa 最喜欢的两个顶点编号。

输出一个整数，表示美丽树的数量，对 $10^9+7$ 取模。

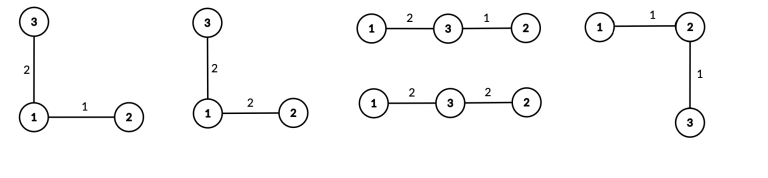
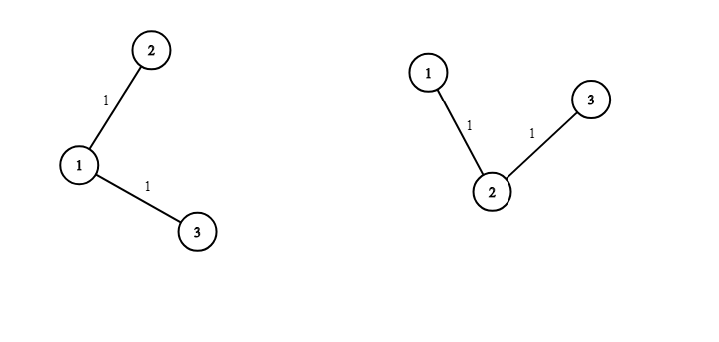
在第一个样例中，有 $5$ 棵美丽树：  在第二个样例中，以下树是美丽的：  由 ChatGPT 4.1 翻译