CF1109F Sasha and Algorithm of Silence's Sounds

一天，Sasha 去公园散步。在公园里，他发现自己最喜欢的长椅被人占了，只好坐在旁边的长椅上。他坐下后，开始聆听寂静。突然，他产生了一个疑问：公园的不同地方，寂静的声音会不会不一样？事实的确如此。我们将公园划分为 $1 \times 1$ 米的方格，称之为单元格。行从上到下编号为 $1$ 到 $n$，列从左到右编号为 $1$ 到 $m$。现在，每个单元格可以用一对整数 $(x, y)$ 表示，其中 $x$ 表示行号，$y$ 表示列号。Sasha 知道，单元格 $(i, j)$ 的寂静程度为 $f_{i,j}$，所有 $f_{i,j}$ 组成了 $1$ 到 $n \cdot m$ 的一个排列。Sasha 决定统计有多少个“愉悦的寂静区间”。 我们取一个区间 $[l \ldots r]$。记 $S$ 为所有满足 $l \le f_{i,j} \le r$ 的单元格 $(i, j)$ 的集合。若对于 $S$ 中任意一对单元格，都只存在一条简单路径将它们连接起来（路径不能经过 $S$ 之外的单元格），则称区间 $[l \ldots r]$ 是“愉悦的”。换句话说，集合 $S$ 在平面上应当构成一棵树。Sasha 很快完成了这个任务，并将算法命名为“寂静之声算法”。 时光流逝，如今只剩下这个算法的传说。为了证明这个故事的真实性，你需要帮助 Sasha，统计不同的愉悦的寂静区间的数量。两个区间 $[l_1 \ldots r_1]$ 和 $[l_2 \ldots r_2]$ 被认为是不同的，当且仅当 $l_1 \neq l_2$ 或 $r_1 \neq r_2$ 或两者都不相等。

第一行包含两个整数 $n$ 和 $m$（$1 \le n, m \le 1000$，$1 \le n \cdot m \le 2 \times 10^5$），表示公园的大小。 接下来的 $n$ 行，每行包含 $m$ 个整数 $f_{i,j}$（$1 \le f_{i,j} \le n \cdot m$），表示编号为 $(i, j)$ 的单元格的寂静程度。 保证所有 $f_{i,j}$ 互不相同。

输出一个整数，表示愉悦的寂静区间的数量。

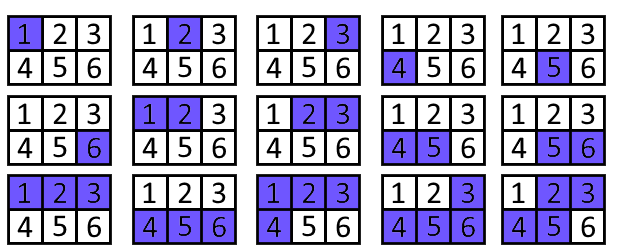
在第一个样例中，所有的寂静区间都是愉悦的。 在第二个样例中，愉悦的寂静区间如下所示：  由 ChatGPT 4.1 翻译