CF1110F Nearest Leaf

我们将树（一个无环连通无向图）的欧拉遍历定义如下：考虑一种深度优先搜索算法，遍历树的顶点，并按访问顺序依次编号（每个顶点只在第一次访问时编号）。该函数从编号为 $1$ 的顶点开始，然后递归地从所有与当前顶点通过一条边相连且尚未访问过的顶点出发，按编号递增的顺序进行。形式化地，你可以用如下伪代码描述该函数： ``` next_id = 1 id = 长度为 n 的数组，初始值均为 -1 visited = 长度为 n 的数组，初始值均为 false function dfs(v): visited[v] = true id[v] = next_id next_id += 1 for to in 按编号递增顺序的 v 的邻居: if not visited[to]: dfs(to) ``` 给定一棵带权树，其顶点已按照上述算法用 $1$ 到 $n$ 的整数编号。 叶子节点是指仅与一个其他顶点相连的顶点。在给定的树中，编号为 $1$ 的顶点不是叶子节点。树中两个顶点之间的距离定义为它们之间简单路径上所有边的权值之和。 你需要回答 $q$ 个如下形式的询问：给定整数 $v$、$l$ 和 $r$，求从顶点 $v$ 到编号在 $l$ 到 $r$（包含端点）之间的某个叶子节点的最短距离。

第一行包含两个整数 $n$ 和 $q$（$3 \leq n \leq 500\,000, 1 \leq q \leq 500\,000$），分别表示树的顶点数和询问数。 接下来的 $n-1$ 行，第 $(i-1)$ 行包含两个整数 $p_i$ 和 $w_i$（$1 \leq p_i < i, 1 \leq w_i \leq 10^9$），表示在顶点 $p_i$ 和 $i$ 之间有一条权值为 $w_i$ 的边。 保证所给边构成一棵树，且顶点编号为欧拉遍历顺序，编号为 $1$ 的顶点不是叶子节点。 接下来的 $q$ 行，每行包含三个整数 $v_i$、$l_i$、$r_i$（$1 \leq v_i \leq n, 1 \leq l_i \leq r_i \leq n$），表示一次询问。保证对于每次询问，区间 $[l_i, r_i]$ 内至少有一个叶子节点。

输出 $q$ 个整数，按输入顺序依次给出每个询问的答案。

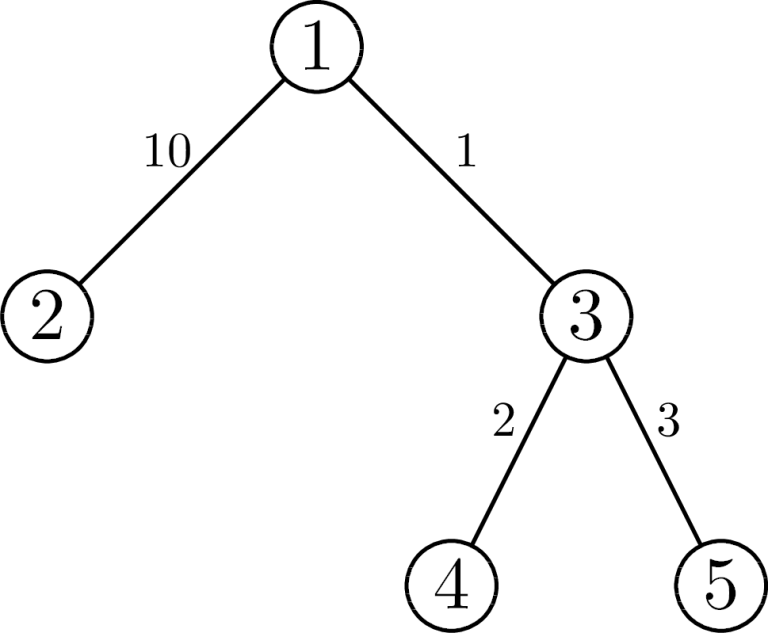
在第一个样例中，树的结构如下：  对于第一个询问，顶点 $1$ 最近的叶子节点是顶点 $4$，距离为 $3$。对于第二个询问，顶点 $5$ 最近的叶子节点是顶点 $5$，距离为 $0$。对于第三个询问，顶点 $4$ 最近的叶子节点是顶点 $4$，但它不在询问区间 $[1, 2]$ 内。区间 $[1, 2]$ 内唯一的叶子节点是顶点 $2$，从顶点 $4$ 到顶点 $2$ 的距离为 $13$。 由 ChatGPT 4.1 翻译