CF1129A2 Toy Train
题目描述
Alice 收到了 Bob 送的一套 Toy Train™ 玩具。它包含一列火车和一个由 $n$ 个车站组成的连通铁路网络,车站编号为 $1$ 到 $n$。火车每次只能停在一个车站,并以环形方式在车站网络中行驶。更具体地说,火车在 $i$ 号车站后会前往 $i+1$ 号车站(当 $1 \leq i < n$),或者如果 $i = n$,则前往 $1$ 号车站。火车前往下一个车站需要 $1$ 秒。
Bob 在离开前给 Alice 留下了一个有趣的任务:用火车将最初分布在某些车站的 $m$ 颗糖果分别送到它们各自的目的地。糖果编号为 $1$ 到 $m$。第 $i$ 颗糖果($1 \leq i \leq m$)现在在 $a_i$ 号车站,需要被送到 $b_i$ 号车站($a_i \neq b_i$)。
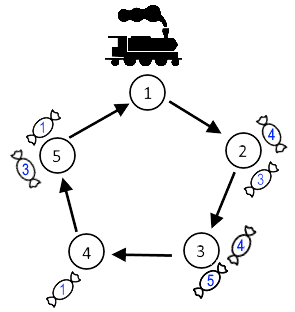 图中糖果上的蓝色数字对应 $b_i$ 的值。图片对应第一个样例。
火车容量无限,可以在任意车站卸下任意数量的糖果。然而,每次火车离开某个车站前,最多只能从该车站装上一颗糖果。你可以选择该车站上的任意一颗糖果装车。装载糖果所需时间可以忽略不计。
现在,Alice 想知道火车需要多少时间才能送完所有糖果。你的任务是,对于每一个车站,计算如果火车从该车站出发,最少需要多少秒才能完成所有糖果的运输任务。
输入格式
第一行包含两个用空格分隔的整数 $n$ 和 $m$($2 \leq n \leq 5000$;$1 \leq m \leq 20000$),分别表示车站数量和糖果数量。
接下来的 $m$ 行中,第 $i$ 行包含两个用空格分隔的整数 $a_i$ 和 $b_i$($1 \leq a_i, b_i \leq n$;$a_i \neq b_i$),分别表示第 $i$ 颗糖果最初所在的车站和目的地车站。
输出格式
输出一行 $n$ 个用空格分隔的整数,第 $i$ 个整数表示如果火车从第 $i$ 号车站出发,最少需要多少秒才能送完所有糖果。
说明/提示
以第二个样例为例:
如果火车从 $1$ 号车站出发,最优策略如下:
1. 装载第一颗糖果。
2. 前往 $2$ 号车站,耗时 $1$ 秒。
3. 卸下第一颗糖果。
4. 前往 $1$ 号车站,耗时 $1$ 秒。
5. 装载第二颗糖果。
6. 前往 $2$ 号车站,耗时 $1$ 秒。
7. 卸下第二颗糖果。
8. 前往 $1$ 号车站,耗时 $1$ 秒。
9. 装载第三颗糖果。
10. 前往 $2$ 号车站,耗时 $1$ 秒。
11. 卸下第三颗糖果。
因此,火车需要 $5$ 秒完成任务。
但如果火车从 $2$ 号车站出发,则需要先移动到 $1$ 号车站才能装载第一颗糖果,这会多耗费 $1$ 秒。因此答案为 $5+1=6$ 秒。
由 ChatGPT 4.1 翻译