CF1130C Connect

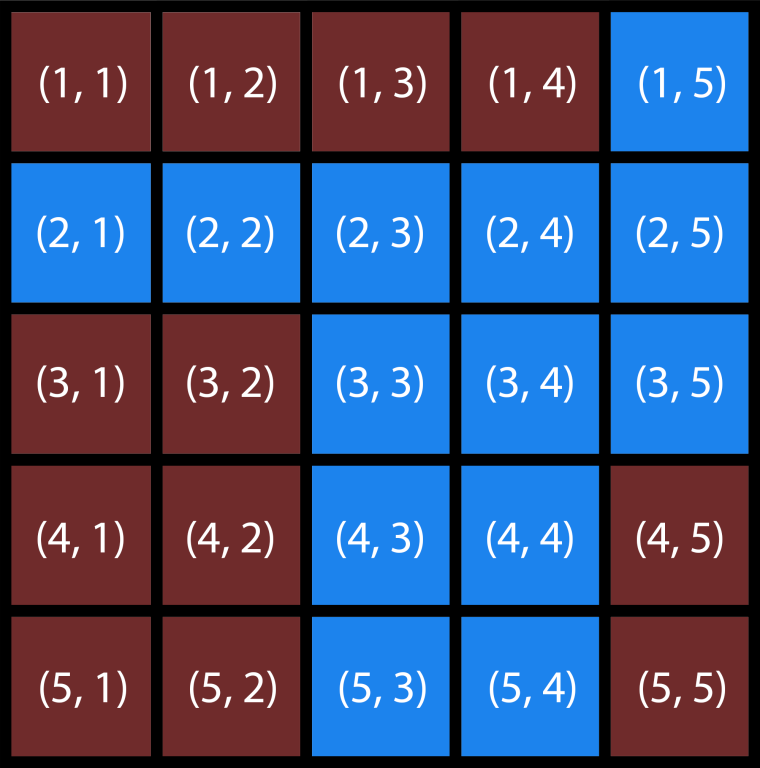
Alice 生活在一个可以用 $n \times n$ 的正方形网格建模的平面星球上，行和列的编号从 $1$ 到 $n$。我们用有序对 $(r, c)$ 表示第 $r$ 行第 $c$ 列的格子。网格中的每个格子要么是陆地，要么是水域。  上图是 $n=5$ 的星球示例，同时也是第一个样例测试的数据。 Alice 居住在陆地格子 $(r_1, c_1)$。她希望前往陆地格子 $(r_2, c_2)$。每次移动时，她可以走到与当前位置相邻的格子之一——即上下左右四个方向。 不幸的是，Alice 不会游泳，也没有其他交通工具（即她只能在陆地上行走）。因此，Alice 的旅行可能无法完成。 为了帮助 Alice，你计划至多在两个陆地格子之间建造一条隧道。通过隧道，Alice 可以自由地在两个端点之间穿梭。当然，建造隧道需要付出代价：在格子 $(r_s, c_s)$ 和 $(r_t, c_t)$ 之间建造隧道的代价为 $(r_s - r_t)^2 + (c_s - c_t)^2$。 现在，你的任务是找出建造至多一条隧道，使得 Alice 能够从 $(r_1, c_1)$ 走到 $(r_2, c_2)$ 的最小可能代价。如果不需要建造隧道，则代价为 $0$。

第一行包含一个整数 $n$（$1 \leq n \leq 50$），表示正方形网格的宽度。 第二行包含两个用空格分隔的整数 $r_1$ 和 $c_1$（$1 \leq r_1, c_1 \leq n$），表示 Alice 所在的格子。 第三行包含两个用空格分隔的整数 $r_2$ 和 $c_2$（$1 \leq r_2, c_2 \leq n$），表示 Alice 希望到达的格子。 接下来的 $n$ 行，每行包含一个长度为 $n$ 的字符串。第 $i$ 行第 $j$ 个字符（$1 \leq i, j \leq n$）为 $0$ 表示 $(i, j)$ 是陆地，为 $1$ 表示 $(i, j)$ 是水域。 保证 $(r_1, c_1)$ 和 $(r_2, c_2)$ 都是陆地。

输出一个整数，表示建造至多一条隧道，使得 Alice 能够从 $(r_1, c_1)$ 走到 $(r_2, c_2)$ 的最小可能代价。

在第一个样例中，应在格子 $(1, 4)$ 和 $(4, 5)$ 之间建造一条隧道。其代价为 $(1-4)^2 + (4-5)^2 = 10$，这是最优方案。这样，Alice 可以从 $(1, 1)$ 走到 $(1, 4)$，通过隧道到达 $(4, 5)$，最后走到 $(5, 5)$。 在第二个样例中，显然应在格子 $(1, 3)$ 和 $(3, 1)$ 之间建造一条隧道。其代价为 $(1-3)^2 + (3-1)^2 = 8$。 由 ChatGPT 4.1 翻译