CF1133F1 Spanning Tree with Maximum Degree

给定一个无向、无权、连通图，该图包含 $n$ 个顶点和 $m$ 条边。保证图中没有自环和重边。 你的任务是找到该图的任意一棵生成树，使得所有顶点中的最大度数尽可能大。这里，顶点的度数指的是与该顶点相连的边的数量。

第一行包含两个整数 $n$ 和 $m$（$2 \le n \le 2 \cdot 10^5$，$n - 1 \le m \le \min(2 \cdot 10^5, \frac{n(n-1)}{2})$），分别表示顶点数和边数。 接下来的 $m$ 行，每行包含两个整数 $v_i$ 和 $u_i$（$1 \le v_i, u_i \le n$，$u_i \ne v_i$），表示一条连接顶点 $v_i$ 和 $u_i$ 的边。图中没有自环和重边，即对于每一对 $(v_i, u_i)$，不存在其他的 $(v_i, u_i)$ 或 $(u_i, v_i)$，且 $v_i \ne u_i$。

输出 $n-1$ 行，每行描述生成树中的一条边。要求输出的生成树边集是输入边集的子集（顺序不限，边 $(v, u)$ 和 $(u, v)$ 视为同一条边）。 如果有多种方案，输出任意一种均可。

第一组样例对应的图示如下： 在本例中，生成树中与顶点 $3$ 相连的边有 $3$ 条，这是所有顶点中的最大度数。很容易看出无法得到更优的答案。 第二组样例对应的图示如下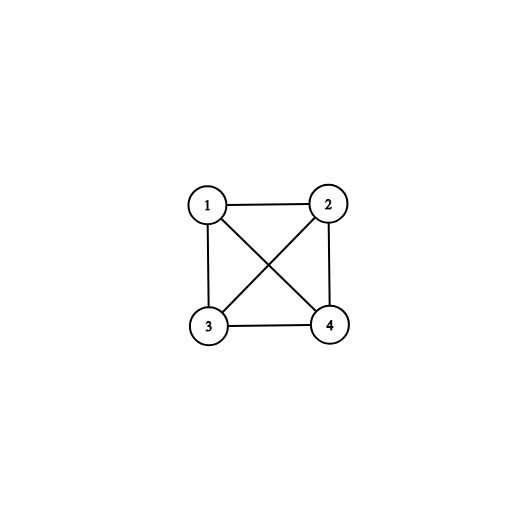： 在本例中，生成树中与顶点 $1$ 相连的边有 $3$ 条，这是所有顶点中的最大度数。很容易看出无法得到更优的答案。 第三组样例对应的图示如下： 在本例中，生成树中与顶点 $2$ 相连的边有 $4$ 条，这是所有顶点中的最大度数。但由于本例具有对称性，也可以选择几乎相同的生成树，只是将顶点 $2$ 换成顶点 $5$。 由 ChatGPT 4.1 翻译