CF1136C Nastya Is Transposing Matrices
题目描述
Nastya 来到她的信息学课堂,她的老师(顺便说一下,这位老师在这里还有点小有名气)给了她如下任务。
给定两个矩阵 $A$ 和 $B$,它们的大小均为 $n \times m$。Nastya 可以对矩阵 $A$ 无限次地执行以下操作:
- 任选 $A$ 的任意一个正方形子矩阵,将其转置(即该子矩阵中原本位于第 $i$ 行第 $j$ 列的元素,在转置后会位于第 $j$ 行第 $i$ 列,且转置后的子矩阵仍保持在原来的位置)。
Nastya 的任务是判断,是否可以通过若干次上述操作将矩阵 $A$ 变换为矩阵 $B$。
正方形子矩阵的定义如下:对于矩阵 $M$,其正方形子矩阵是指由 $M$ 的某些连续行 $x, x+1, \dots, x+k-1$ 和连续列 $y, y+1, \dots, y+k-1$ 组成的 $k \times k$ 子矩阵。换句话说,正方形子矩阵是原矩阵中不带空洞的一个正方形区域。
下图为操作示例:
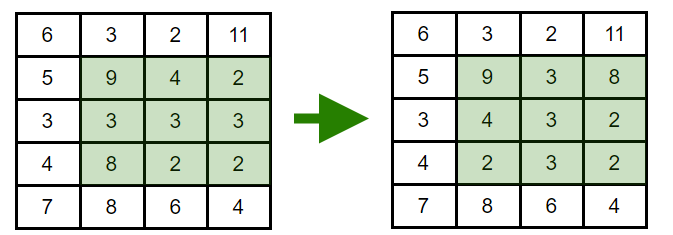
由于可能需要大量操作,请你帮助 Nastya 判断是否可以完成目标。
输入格式
第一行包含两个整数 $n$ 和 $m$,用空格分隔($1 \leq n, m \leq 500$),表示矩阵 $A$ 和 $B$ 的行数和列数。
接下来的 $n$ 行,每行包含 $m$ 个整数,第 $i$ 行第 $j$ 个数表示矩阵 $A$ 第 $i$ 行第 $j$ 列的元素($1 \leq A_{ij} \leq 10^{9}$)。
再接下来的 $n$ 行,每行包含 $m$ 个整数,第 $i$ 行第 $j$ 个数表示矩阵 $B$ 第 $i$ 行第 $j$ 列的元素($1 \leq B_{ij} \leq 10^{9}$)。
输出格式
如果可以通过若干次操作将 $A$ 变换为 $B$,输出 "YES"(不带引号);否则输出 "NO"(不带引号)。
你可以使用大写或小写字母输出。
说明/提示
以第三个样例为例,初始时矩阵 $A$ 如下:
$$
\begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{bmatrix}
$$
然后我们选择整个矩阵作为转置的子矩阵,得到:
$$
\begin{bmatrix}
1 & 4 & 7\\
2 & 5 & 8\\
3 & 6 & 9
\end{bmatrix}
$$
接着我们对以 $(2, 2)$ 和 $(3, 3)$ 为角的子矩阵进行转置:
$$
\begin{bmatrix}
1 & 4 & 7\\
2 & \textbf{5} & \textbf{8}\\
3 & \textbf{6} & \textbf{9}
\end{bmatrix}
$$
于是矩阵变为:
$$
\begin{bmatrix}
1 & 4 & 7\\
2 & 5 & 6\\
3 & 8 & 9
\end{bmatrix}
$$
这就是 $B$。
由 ChatGPT 4.1 翻译