CF1136C Nastya Is Transposing Matrices

Nastya came to her informatics lesson, and her teacher who is, by the way, a little bit famous here gave her the following task. Two matrices $ A $ and $ B $ are given, each of them has size $ n \times m $ . Nastya can perform the following operation to matrix $ A $ unlimited number of times: - take any square square submatrix of $ A $ and transpose it (i.e. the element of the submatrix which was in the $ i $ -th row and $ j $ -th column of the submatrix will be in the $ j $ -th row and $ i $ -th column after transposing, and the transposed submatrix itself will keep its place in the matrix $ A $ ). Nastya's task is to check whether it is possible to transform the matrix $ A $ to the matrix $ B $ . 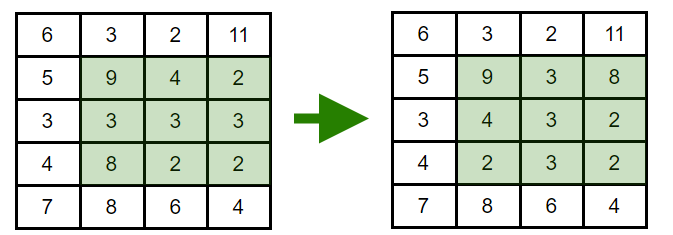Example of the operationAs it may require a lot of operations, you are asked to answer this question for Nastya. A square submatrix of matrix $ M $ is a matrix which consist of all elements which comes from one of the rows with indeces $ x, x+1, \dots, x+k-1 $ of matrix $ M $ and comes from one of the columns with indeces $ y, y+1, \dots, y+k-1 $ of matrix $ M $ . $ k $ is the size of square submatrix. In other words, square submatrix is the set of elements of source matrix which form a solid square (i.e. without holes).

The first line contains two integers $ n $ and $ m $ separated by space ( $ 1 \leq n, m \leq 500 $ ) — the numbers of rows and columns in $ A $ and $ B $ respectively. Each of the next $ n $ lines contains $ m $ integers, the $ j $ -th number in the $ i $ -th of these lines denotes the $ j $ -th element of the $ i $ -th row of the matrix $ A $ ( $ 1 \leq A_{ij} \leq 10^{9} $ ). Each of the next $ n $ lines contains $ m $ integers, the $ j $ -th number in the $ i $ -th of these lines denotes the $ j $ -th element of the $ i $ -th row of the matrix $ B $ ( $ 1 \leq B_{ij} \leq 10^{9} $ ).

Print "YES" (without quotes) if it is possible to transform $ A $ to $ B $ and "NO" (without quotes) otherwise. You can print each letter in any case (upper or lower).

Consider the third example. The matrix $ A $ initially looks as follows. $ $$$ \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} $ $

Then we choose the whole matrix as transposed submatrix and it becomes

$ $ \begin{bmatrix} 1 & 4 & 7\\ 2 & 5 & 8\\ 3 & 6 & 9 \end{bmatrix} $ $

Then we transpose the submatrix with corners in cells $ (2, 2) $ and $ (3, 3) $ .

$ $ \begin{bmatrix} 1 & 4 & 7\\ 2 & \textbf{5} & \textbf{8}\\ 3 & \textbf{6} & \textbf{9} \end{bmatrix} $ $

So matrix becomes

$ $ \begin{bmatrix} 1 & 4 & 7\\ 2 & 5 & 6\\ 3 & 8 & 9 \end{bmatrix} $ $

and it is $ B$$$.