CF1137A Skyscrapers
题目描述
Dora 非常喜欢冒险。在一次旅行中,她遇到了一座神奇的城市,这座城市由 $n$ 条东西方向的街道和 $m$ 条南北方向的街道组成。自然地,这座城市有 $nm$ 个交叉口。在每一个第 $i$ 条东西街道与第 $j$ 条南北街道的交叉口上,都有一座宏伟的摩天大楼。Dora 立刻产生了好奇心,决定探索这座城市建筑的高度。
当 Dora 经过第 $i$ 条东西街道与第 $j$ 条南北街道的交叉口时,她会考察这两条街道。在 Dora 了解了这两条街道上所有摩天大楼的高度后,她会思考:如何重新分配这两条街道上摩天大楼的高度,使得最大高度尽可能小,并且任意两座摩天大楼在同一条街道上的高度比较结果不发生变化。
具体来说,在每一个 $nm$ 个交叉口,Dora 都要独立地解决这样一个问题。她会看到 $n + m - 1$ 座摩天大楼,并且知道它们的实际高度。对于任意两座摩天大楼的高度,都可以比较出“更高”、“更低”或“相等”。现在 Dora 想选择一个整数 $x$,并将每座摩天大楼的高度重新赋值为 $1$ 到 $x$ 之间的某个整数。在赋值时,Dora 希望保持这两条街道上摩天大楼的相对高度顺序不变。也就是说,在当前东西街道上任意两座摩天大楼的高度比较结果不能改变,在当前南北街道上任意两座摩天大楼的高度比较结果也不能改变。注意,南北街道上的摩天大楼不会与东西街道上的摩天大楼进行比较,只有交叉口上的摩天大楼会同时与两条街道上的摩天大楼进行比较。对于每一个交叉口,Dora 都要独立地计算出最小可能的 $x$。
例如,若某个交叉口及其对应的两条街道如下所示:
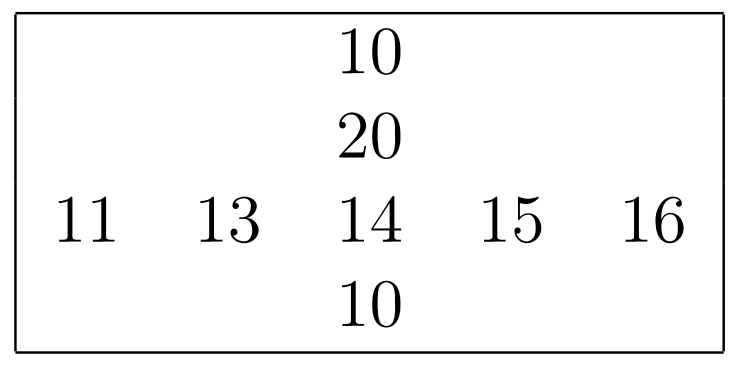
那么最优的做法是将摩天大楼的高度替换如下(注意所有在东西街道和南北街道内部的“更小”、“相等”、“更大”关系都被保留):
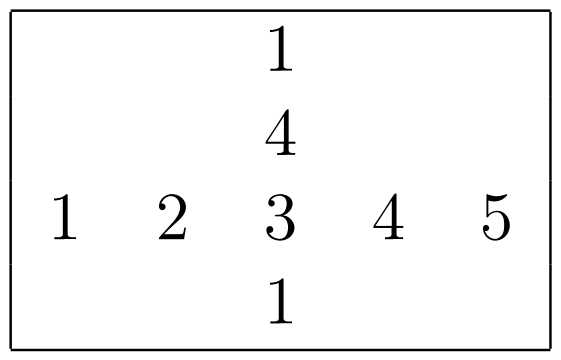
使用的最大数字是 $5$,因此该交叉口的答案为 $5$。
请你帮助 Dora 计算每一个交叉口的答案。
输入格式
第一行包含两个整数 $n$ 和 $m$($1 \le n, m \le 1000$),分别表示东西方向和南北方向的街道数量。
接下来的 $n$ 行,每行包含 $m$ 个整数 $a_{i,1}, a_{i,2}, \ldots, a_{i,m}$($1 \le a_{i,j} \le 10^9$)。第 $i$ 行第 $j$ 个数 $a_{i,j}$ 表示第 $i$ 条东西街道与第 $j$ 条南北街道交叉口的摩天大楼高度。
输出格式
输出 $n$ 行,每行 $m$ 个整数。第 $i$ 行第 $j$ 个数 $x_{i,j}$ 表示第 $i$ 条东西街道与第 $j$ 条南北街道交叉口的答案。
说明/提示
在第一个样例中,对于每个交叉口,都无法进一步减小最大使用的高度,因此不需要更改任何高度。
在第二个样例中,答案如下:
- 第一行第一列交叉口的答案: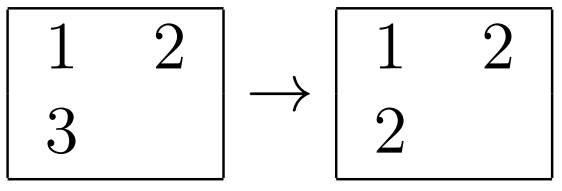
- 第一行第二列交叉口的答案: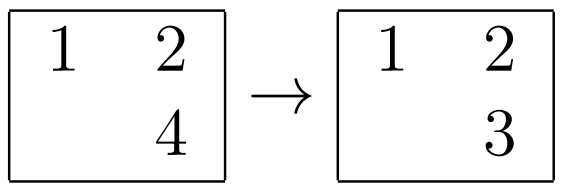
- 第二行第一列交叉口的答案: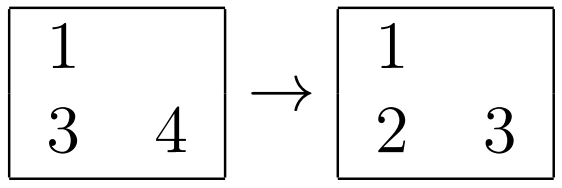
- 第二行第二列交叉口的答案: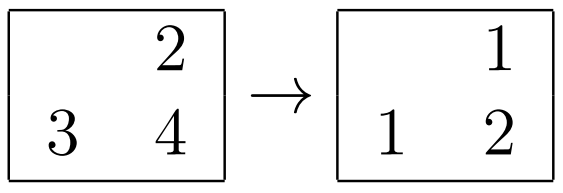
由 ChatGPT 4.1 翻译