CF1139C Edgy Trees
题目描述
给定一棵有 $n$ 个顶点的树(一个无环连通无向图)。树的 $n-1$ 条边中,每条边都被染成黑色或红色。
你还得到一个整数 $k$。考虑长度为 $k$ 的顶点序列。我们称一个序列 $[a_1, a_2, \ldots, a_k]$ 是好的,如果它满足以下条件:
- 我们将在树上行走一条路径(可能多次经过同一条边或顶点),从 $a_1$ 出发,最终到达 $a_k$。
- 从 $a_1$ 出发,走到 $a_2$,采用 $a_1$ 和 $a_2$ 之间的最短路径;然后以同样的方式走到 $a_3$,依此类推,直到你走完 $a_{k-1}$ 到 $a_k$ 之间的最短路径。
- 如果在这个过程中至少经过了一条黑色边,则该序列是好的。
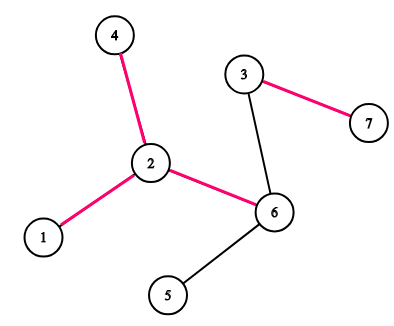
考虑上图中的树。如果 $k=3$,则以下序列是好的:$[1, 4, 7]$,$[5, 5, 3]$ 和 $[2, 3, 7]$。以下序列不是好的:$[1, 4, 6]$,$[5, 5, 5]$,$[3, 7, 3]$。
共有 $n^k$ 个长度为 $k$ 的顶点序列,请你计算其中有多少个是好的。由于答案可能很大,请输出答案对 $10^9+7$ 取模后的结果。
输入格式
第一行包含两个整数 $n$ 和 $k$($2 \le n \le 10^5$,$2 \le k \le 100$),分别表示树的大小和顶点序列的长度。
接下来的 $n-1$ 行,每行包含三个整数 $u_i$、$v_i$ 和 $x_i$($1 \le u_i, v_i \le n$,$x_i \in \{0, 1\}$),表示一条边的两个端点和该边的颜色($0$ 表示红色,$1$ 表示黑色)。
输出格式
输出好的序列数量,对 $10^9+7$ 取模。
说明/提示
在第一个样例中,所有长度为 $4$ 的序列(共 $4^4$ 个)中,除了以下序列之外,其他都是好的:
- $[1, 1, 1, 1]$
- $[2, 2, 2, 2]$
- $[3, 3, 3, 3]$
- $[4, 4, 4, 4]$
在第二个样例中,所有边都是红色,因此没有好的序列。
由 ChatGPT 4.1 翻译