CF1141G Privatization of Roads in Treeland

Treeland 有 $n$ 个城市和 $n-1$ 条道路。每条道路都是双向的，连接着两个不同的城市。从任意一个城市出发，都可以通过道路到达其他任意城市。没错，这个国家的地形结构是一棵无向树。 Treeland 有一些私营公路公司。政府决定将道路出售给这些公司。每条道路将归属于一家公路公司，一个公司可以拥有多条道路。 政府担心被认为不公平。他们认为，如果某个城市有一家公路公司拥有两条或以上通往该城市的道路，那么该城市的居民可能会觉得政府不公平。政府希望进行这样的私有化分配：使得拥有两条或以上同一公司道路的城市数量不超过 $k$，并且参与私有化的公司数量尽可能少。 请选择一个公司数 $r$，使得可以将每条道路分配给 $1$ 到 $r$ 号公司中的一家，并且满足拥有两条或以上同一公司道路的城市数量至多为 $k$。换句话说，如果某个城市的所有道路都归属于不同的公司，则该城市是“好”的。你的任务是找到最小的 $r$，使得存在一种分配方案，使得“不好”的城市数量不超过 $k$。 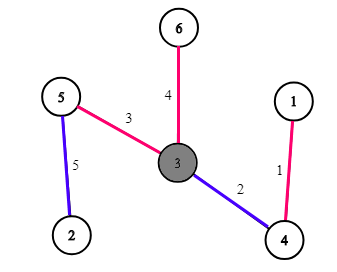 上图展示了第一个样例（$n=6, k=2$）。答案是 $r=2$ 家公司。边上的数字表示边的编号，边的颜色表示公司：红色对应第一家公司，蓝色对应第二家公司。灰色的顶点（编号 $3$）是“不好”的城市。这类城市的数量（只有一个）不超过 $k=2$。如果只有一家公司的话，不可能让“不好”的城市数量不超过 $k=2$。

第一行包含两个整数 $n$ 和 $k$（$2 \le n \le 200000, 0 \le k \le n - 1$），分别表示城市数量和最多允许有多少个“不好”的城市。 接下来的 $n-1$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$1 \le x_i, y_i \le n$），表示第 $i$ 条道路连接着城市 $x_i$ 和 $y_i$。

第一行输出所需的公司数 $r$（$1 \le r \le n-1$）。 第二行输出 $n-1$ 个整数 $c_1, c_2, \dots, c_{n-1}$（$1 \le c_i \le r$），其中 $c_i$ 表示第 $i$ 条道路归属于哪家公司。如果有多种方案，输出任意一种均可。

由 ChatGPT 4.1 翻译