CF1142C U2

最近，Vasya 得知，对于任意两个 $x$ 坐标不同的点，可以唯一确定一条形如 $y = x^2 + bx + c$ 的抛物线，其中 $b$ 和 $c$ 为实数。我们称这样的抛物线为 $U$ 形抛物线。 Vasya 在平面上画了若干个具有整数坐标的不同点，然后对于每一对 $x$ 坐标不同的点，画出一条经过这两点的 $U$ 形抛物线。图画变得有些杂乱，但 Vasya 仍然想统计，有多少条画出的抛物线，其内部区域内没有任何一个已画出的点。请你帮助 Vasya 计算。 $U$ 形抛物线的内部区域，指的是当 $y$ 轴向上时，平面上严格在该抛物线上方的部分。

第一行包含一个整数 $n$（$1 \le n \le 100\,000$），表示点的数量。 接下来的 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$，表示第 $i$ 个点的坐标。保证所有点互不相同，且坐标的绝对值不超过 $10^6$。

输出一行一个整数，表示经过至少两个给定点且其内部区域不包含任何给定点（不包括抛物线本身）的 $U$ 形抛物线的数量。

下图中展示了每个样例中所有经过至少两个给定点的 $U$ 形抛物线。没有任何给定点在其内部区域的 $U$ 形抛物线用红色表示。 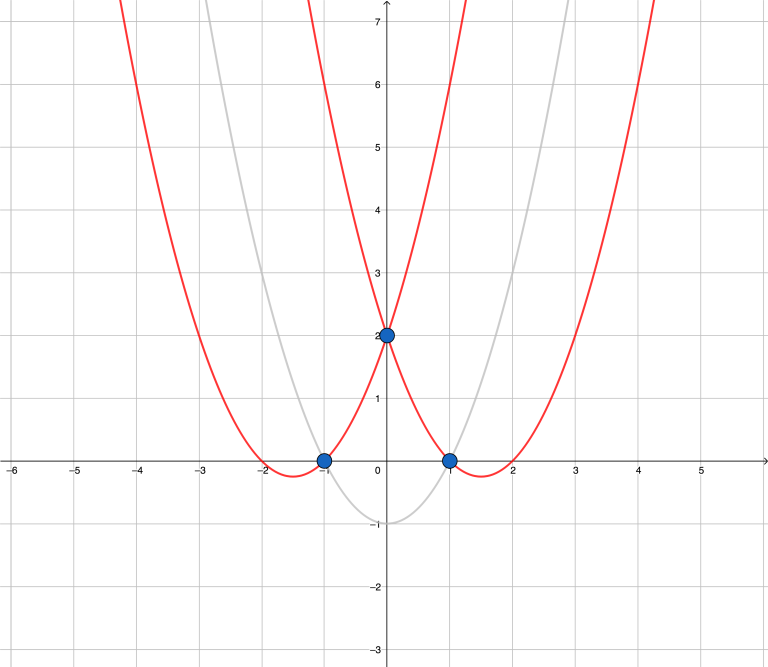 第一个样例。 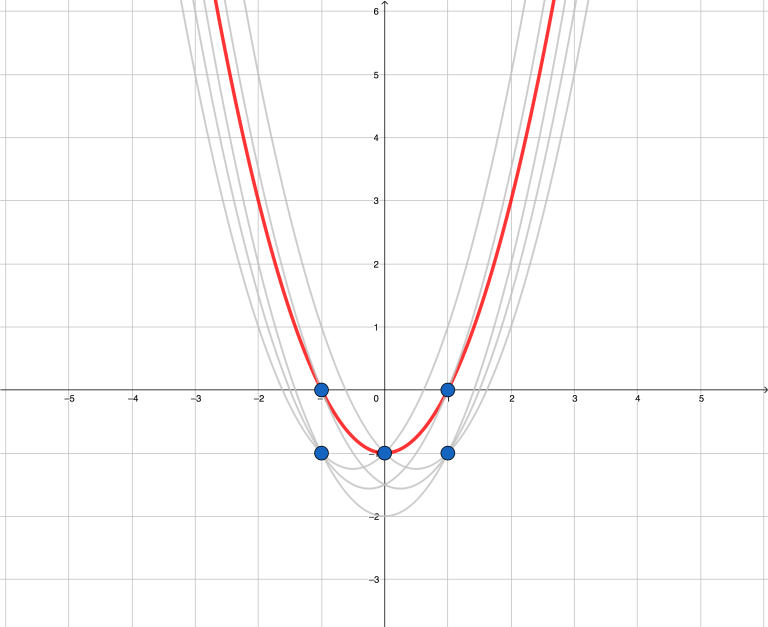 第二个样例。 由 ChatGPT 4.1 翻译