CF1146F Leaf Partition

给定一棵有 $n$ 个节点的有根树，节点编号为 $1$ 到 $n$，树的根为节点 $1$。第 $i$ 个节点的父节点为 $p_i$。叶子节点是没有子节点的节点。对于给定的叶子节点集合 $L$，定义 $f(L)$ 为包含所有叶子节点 $L$ 的最小连通子图。 你希望将所有叶子节点划分为若干组，使得对于任意两个不同的组 $x, y$，$f(x)$ 和 $f(y)$ 互不相交。 请计算有多少种划分叶子节点的方案，答案对 $998244353$ 取模。如果存在两种方案，使得存在两个叶子节点在一种方案中属于同一组，在另一种方案中属于不同组，则认为这两种方案不同。

第一行包含一个整数 $n$（$2 \leq n \leq 200\,000$），表示树的节点数。 第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$（$1 \leq p_i < i$）。

输出一个整数，表示划分叶子节点的方案数，对 $998244353$ 取模。

在第一个样例中，叶子节点为 $2,3,4,5$。划分叶子节点的方案如下图所示。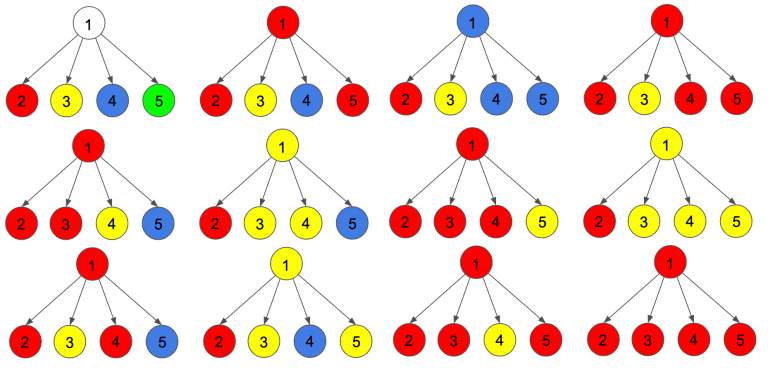 在第二个样例中，唯一的叶子节点是 $10$，因此只有一种划分方案。注意节点 $1$ 不是叶子节点。 由 ChatGPT 4.1 翻译