CF1146H Satanic Panic
题目描述
给定平面上的 $n$ 个点,保证没有三点共线。
一个五角星是指从这 $n$ 个点中选出 $5$ 个点 $A,B,C,D,E$,并且可以按如下方式排列。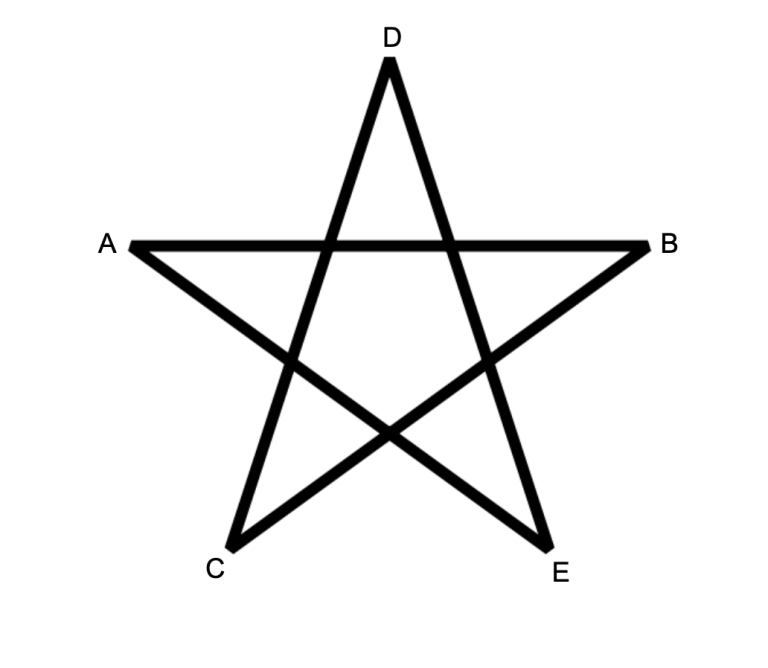 注意,线段的长度无关紧要,只要存在图中所示的特定交点即可。
请计算从给定点集中选出 $5$ 个点组成五角星的方案数。
输入格式
第一行包含一个整数 $n$($5 \leq n \leq 300$),表示点的数量。
接下来的 $n$ 行,每行包含两个整数 $x_i, y_i$($-10^6 \leq x_i, y_i \leq 10^6$),表示第 $i$ 个点的坐标。保证没有三点共线。
输出格式
输出一个整数,表示可以组成五角星的 $5$ 个点的集合数量。
说明/提示
第一个样例的示意图如下:
第二个样例的示意图如下:
第三个样例的示意图如下:
由 ChatGPT 4.1 翻译