CF1146H Satanic Panic

You are given a set of $ n $ points in a 2D plane. No three points are collinear. A pentagram is a set of $ 5 $ points $ A,B,C,D,E $ that can be arranged as follows. 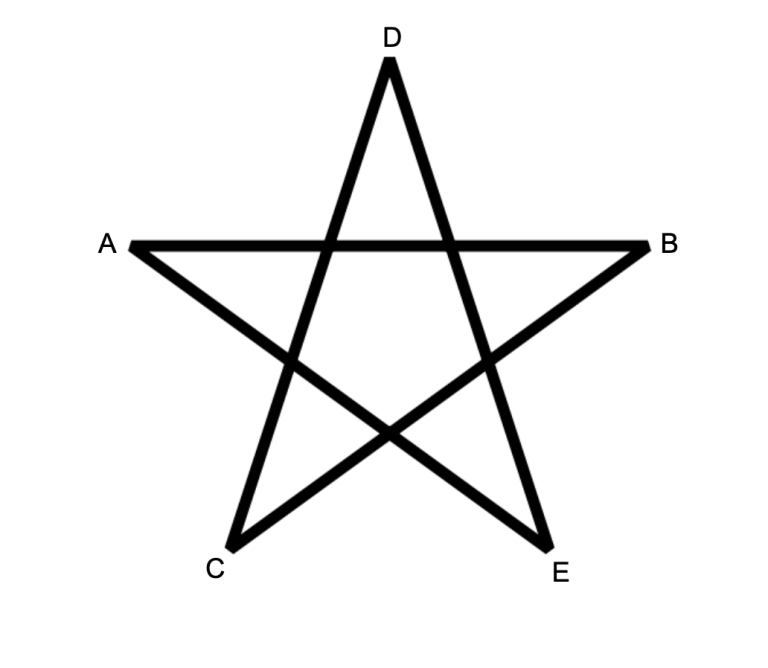 Note the length of the line segments don't matter, only that those particular intersections exist. Count the number of ways to choose $ 5 $ points from the given set that form a pentagram.

The first line contains an integer $ n $ ( $ 5 \leq n \leq 300 $ ) — the number of points. Each of the next $ n $ lines contains two integers $ x_i, y_i $ ( $ -10^6 \leq x_i,y_i \leq 10^6 $ ) — the coordinates of the $ i $ -th point. It is guaranteed that no three points are collinear.

Print a single integer, the number of sets of $ 5 $ points that form a pentagram.

A picture of the first sample:  A picture of the second sample:  A picture of the third sample: