CF1147B Chladni Figure

Inaka 有一个圆盘，其周长为 $n$ 个单位。圆周上等距分布着 $n$ 个点，顺时针编号为 $1$ 到 $n$，其中第 $i$ 个点与第 $i+1$ 个点（$1 \leq i < n$）相邻，第 $n$ 个点与第 $1$ 个点也相邻。 圆盘上有 $m$ 条直线段，这些线段的两个端点都在上述 $n$ 个点中。 Inaka 想知道她的图像是否具有旋转对称性。也就是说，是否存在一个整数 $k$（$1 \leq k < n$），使得将所有线段沿圆心顺时针旋转 $k$ 个单位后，得到的新图像与原图像完全相同。

第一行包含两个用空格分隔的整数 $n$ 和 $m$（$2 \leq n \leq 100\,000$，$1 \leq m \leq 200\,000$），分别表示点的数量和线段的数量。 接下来的 $m$ 行中，第 $i$ 行包含两个用空格分隔的整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq n$，$a_i \neq b_i$），表示一条连接点 $a_i$ 和 $b_i$ 的线段。 保证没有两条线段完全重合。

输出一行，如果图像具有旋转对称性，则输出 "Yes"；否则输出 "No"（不含引号）。 你可以以任意大小写输出每个字母。

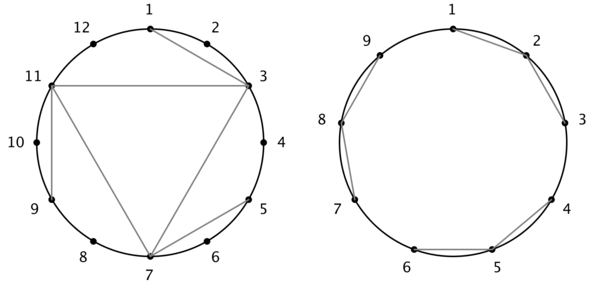
前两个样例如下图所示。两个图像都可以通过顺时针旋转 $120$ 度后与原图像重合。  由 ChatGPT 4.1 翻译