CF1147B Chladni Figure

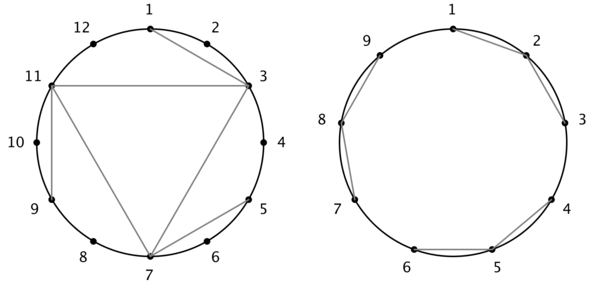
Inaka has a disc, the circumference of which is $ n $ units. The circumference is equally divided by $ n $ points numbered clockwise from $ 1 $ to $ n $ , such that points $ i $ and $ i + 1 $ ( $ 1 \leq i < n $ ) are adjacent, and so are points $ n $ and $ 1 $ . There are $ m $ straight segments on the disc, the endpoints of which are all among the aforementioned $ n $ points. Inaka wants to know if her image is rotationally symmetrical, i.e. if there is an integer $ k $ ( $ 1 \leq k < n $ ), such that if all segments are rotated clockwise around the center of the circle by $ k $ units, the new image will be the same as the original one.

The first line contains two space-separated integers $ n $ and $ m $ ( $ 2 \leq n \leq 100\,000 $ , $ 1 \leq m \leq 200\,000 $ ) — the number of points and the number of segments, respectively. The $ i $ -th of the following $ m $ lines contains two space-separated integers $ a_i $ and $ b_i $ ( $ 1 \leq a_i, b_i \leq n $ , $ a_i \neq b_i $ ) that describe a segment connecting points $ a_i $ and $ b_i $ . It is guaranteed that no segments coincide.

Output one line — "Yes" if the image is rotationally symmetrical, and "No" otherwise (both excluding quotation marks). You can output each letter in any case (upper or lower).

The first two examples are illustrated below. Both images become the same as their respective original ones after a clockwise rotation of $ 120 $ degrees around the center.