CF1149C Tree Generator™

Owl Pacino 一直对树结构情有独钟——尤其是无权有根树。他喜欢为每棵树求直径——即树中任意简单路径的最大长度。 Owl Pacino 的猫头鹰朋友们决定送给他一台 Tree Generator™——这是一台能够根据描述生成有根树的强大机器。一棵 $n$ 个结点的有根树可以用长度为 $2(n-1)$ 的括号序列来描述，具体方式如下：找到一条从根结点出发并最终回到根结点的路径，要求每条边恰好经过两次——一次向下走，一次向上走。沿着这条路径，每当沿着一条边向下时，记下一个左括号“(”；每当沿着一条边向上时，记下一个右括号“)” 。 下图展示了样例有根树及其描述：  Owl 写下了一棵 $n$ 个结点的有根树的描述。之后，他又写了 $q$ 次新的描述。每次写新描述时，他会从上一次写下的描述中选出两个不同的位置，交换这两个括号，并将结果写下来。他始终确保每次写下的字符串都能描述一棵有根树。 每次写下描述后，Pacino 都用 Tree Generator™ 生成对应的树。请你求出每次生成的树的直径。

输入的第一行包含两个整数 $n, q$（$3 \leq n \leq 100\,000$，$1 \leq q \leq 100\,000$），分别表示树的结点数和描述被修改的次数。第二行包含初始树的描述——一个长度为 $2(n-1)$ 的括号序列，仅由左括号“(”和右括号“)”组成。 接下来的 $q$ 行，每行描述一次修改，包含两个用空格分隔的整数 $a_i, b_i$（$2 \leq a_i, b_i \leq 2n-3$），表示要交换的两个括号的位置。可以保证每次修改后描述都会发生变化，并且每次修改后括号序列都能描述一棵有根树。

输出 $q+1$ 个整数，依次表示每次生成的树的直径。

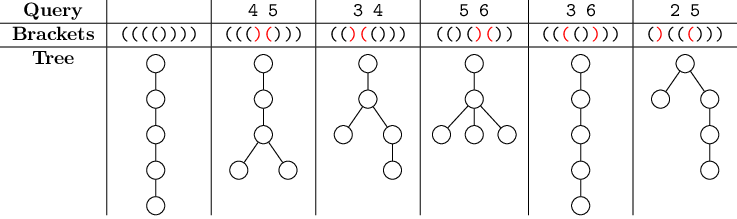
下图展示了第一个样例测试中每次生成的树及其描述：  由 ChatGPT 4.1 翻译