CF1153D Serval and Rooted Tree

现在 Serval 是 Japari 中学的一名初中生，他依然像以前一样热爱数学。 作为一个有天赋的数学少年，他喜欢玩数字游戏。这一次，他想在一棵有根树上玩数字游戏。 一棵树是一个无环连通图。有根树有一个特殊的顶点称为根节点。节点 $v$ 的父节点是从根到 $v$ 的路径上，最后一个不同于 $v$ 的顶点。节点 $v$ 的所有以 $v$ 为父节点的节点称为 $v$ 的子节点。如果一个节点没有子节点，则称其为叶子节点。 Serval 拥有的这棵有根树有 $n$ 个节点，节点 $1$ 是根节点。Serval 会在树的所有节点上写上一些数字。不过，有一些限制。每个非叶子节点上都写有一个操作 $\max$ 或 $\min$，表示该节点上的数字应等于其所有子节点上的数字的最大值或最小值。 假设树上有 $k$ 个叶子节点。Serval 想将整数 $1, 2, \ldots, k$ 分别填入这 $k$ 个叶子节点（每个数字只能用一次）。他喜欢大的数字，所以他希望根节点上的数字尽可能大。作为他最好的朋友，你能帮帮他吗？

第一行包含一个整数 $n$（$2 \leq n \leq 3 \cdot 10^5$），表示树的节点数。 第二行包含 $n$ 个整数，第 $i$ 个整数表示第 $i$ 个节点上的操作。$0$ 表示 $\min$，$1$ 表示 $\max$。如果该节点是叶子节点，依然会给出 $0$ 或 $1$，但可以忽略。 第三行包含 $n-1$ 个整数 $f_2, f_3, \ldots, f_n$（$1 \leq f_i \leq i-1$），其中 $f_i$ 表示第 $i$ 个节点的父节点编号。

输出一个整数，表示根节点上可能取得的最大数字。

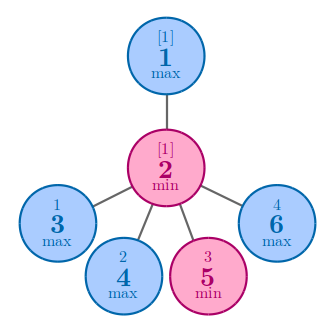
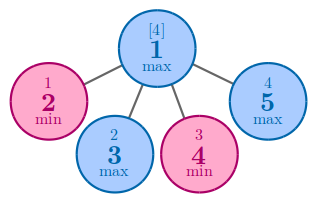
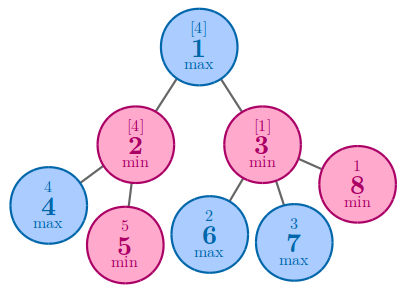
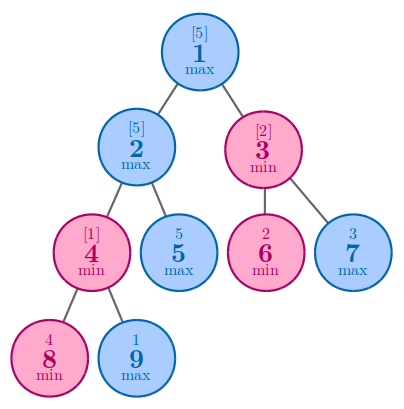
下图解释了样例。节点中间的数字是节点编号，节点上方的数字是节点中的数字。 在第一个样例中，无论如何安排数字，答案都是 $1$。  在第二个样例中，无论如何安排数字，答案都是 $4$。  在第三个样例中，为了得到 $4$，一种最优方案是将 $4$ 和 $5$ 分别放在节点 $4$ 和 $5$ 上。  在第四个样例中，最优方案是将 $5$ 放在节点 $5$ 上。  由 ChatGPT 4.1 翻译