CF1155F Delivery Oligopoly
题目描述
整个 Berland 的快递市场由两家竞争公司 BerEx 和 BerPS 控制。它们都在 Berland 的所有城市间提供快速且可靠的快递服务。
Berland 的地图可以表示为一张无向图,城市为顶点,道路为连接城市之间的边。任意一对城市之间最多只有一条道路,每条道路连接的是不同的城市。
BerEx 和 BerPS 之间竞争激烈,对于每一对城市 $(v, u)$,它们都设置了各自的路径,使得这两条路径之间没有任何一条道路是重合的。保证这样的设置是可行的。
现在,Berland 政府决定通过废弃部分道路来减少道路维护成本。显然,他们希望维护的道路数量尽可能少。但同时,他们又不希望破坏整个快递系统。因此,BerEx 和 BerPS 之间每一对城市之间仍然需要能够有两条不重合的路径。
请问 Berland 政府最少需要维护多少条道路?
更正式地说,给定一张 $2$-边连通的无向图,最少可以保留多少条边,使得保留后的图依然是 $2$-边连通的?
输入格式
第一行包含两个整数 $n$ 和 $m$($3 \le n \le 14$,$n \le m \le \frac{n(n - 1)}{2}$),分别表示城市数量和道路数量。
接下来的 $m$ 行,每行包含两个整数 $v$ 和 $u$($1 \le v, u \le n$,$v \ne u$),表示一条连接城市 $v$ 和 $u$ 的道路。
保证任意一对城市之间最多只有一条道路。保证任意一对城市之间都至少存在两条不重合的路径。
输出格式
第一行输出一个整数 $k$,表示 Berland 政府最少需要维护的道路数量。
接下来的 $k$ 行,每行输出两个整数 $v$ 和 $u$,表示被维护的道路连接的两个城市。
如果有多组最优解,输出任意一组即可。道路输出顺序不限。
说明/提示
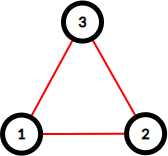
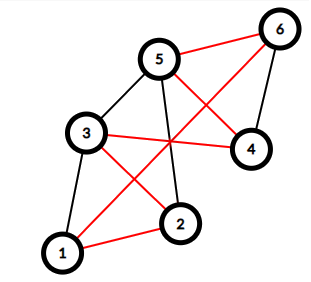
以下是样例中的图示,红色边为被维护的道路。

由 ChatGPT 4.1 翻译