CF1156A Inscribed Figures
题目描述
伯兰国立大学数学系发现新生的数学能力急剧下降。今年入学数学测试的最高分只有 8 分,满分可是 100 分!因此,决定让测试变得更简单。
未来的学生只需要回答一个问题。他们会得到一个整数序列 $a_1, a_2, \dots, a_n$,每个数字都是 $1$ 到 $3$ 之间的整数,且对于每个合法的 $i$,都有 $a_i \ne a_{i+1}$。第 $i$ 个数字表示第 $i$ 个图形的类型:
1. 圆;
2. 等腰三角形(高等于底边长度);
3. 正方形。
这些给定顺序的图形被放置在某个平面直角坐标系中,满足以下条件:
- 第 $i+1$ 个图形被内切于第 $i$ 个图形;
- 每个三角形的底边平行于 $OX$ 轴;
- 三角形的顶点(与底边相对的那个)朝上;
- 每个正方形的边都平行于坐标轴;
- 对于每个 $i$ 从 $2$ 到 $n$,第 $i$ 个图形的边长(对于三角形和正方形)或半径(对于圆)都尽可能大。
注意,对于给定的第一个图形的位置和大小,这种构造方式是唯一的。
你的任务是计算所有图形之间接触的不同点的数量(这些点不一定是整数坐标)。但要注意,有时这些接触点的数量是无限的。不过,这对你来说应该不难吧?
你能通过这道数学测试,顺利进入伯兰国立大学吗?
输入格式
第一行包含一个整数 $n$($2 \le n \le 100$),表示图形的数量。
第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$($1 \le a_i \le 3$,$a_i \ne a_{i+1}$),表示每个图形的类型。
输出格式
第一行输出 "Infinite"(如果接触点的数量是无限的),否则输出 "Finite"。
如果是有限的情况,第二行输出不同接触点的数量。保证答案不会超过 32 位整数范围。
说明/提示
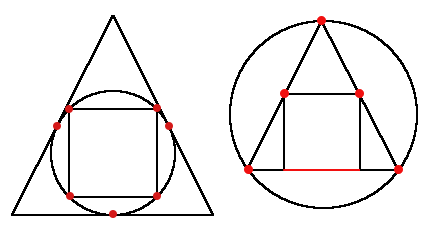
以下是样例的示意图。注意,三角形不是等边三角形,而是等腰三角形(高等于底边长度),因此它能以唯一的方式内切于正方形。
不同的接触点用红色标记。
在第二个样例中,三角形和正方形之间的接触是一整条线段,因此接触点是无限的。
由 ChatGPT 4.1 翻译