CF1158D Winding polygonal line

Vasya 在平面上有 $n$ 个不同的点 $A_1, A_2, \ldots, A_n$。任意三点不共线。他希望将这些点按某种顺序排列为 $A_{p_1}, A_{p_2}, \ldots, A_{p_n}$，其中 $p_1, p_2, \ldots, p_n$ 是 $1$ 到 $n$ 的某个排列。 随后，他将在这些点上画一条有向折线，依次从每个点连向下一个点。也就是说，对于所有 $1 \leq i \leq n-1$，他会从点 $A_{p_i}$ 画一条有向线段到点 $A_{p_{i+1}}$。他希望这条折线满足以下两个条件： - 折线不自交，即任意两条非相邻的线段没有公共点。 - 折线是“绕行”的。 Vasya 有一个长度为 $n-2$ 的字符串 $s$，由字母 "L" 或 "R" 组成。我们称一条有向折线为“绕行”的，如果其第 $i$ 次转弯是左转当且仅当 $s_i = $ "L"，右转当且仅当 $s_i = $ "R"。更正式地说：第 $i$ 次转弯发生在点 $A_{p_{i+1}}$，此时有向线段从 $A_{p_i}$ 到 $A_{p_{i+1}}$，再从 $A_{p_{i+1}}$ 到 $A_{p_{i+2}}$。设 $\overrightarrow{v_1} = \overrightarrow{A_{p_i}A_{p_{i+1}}}$，$\overrightarrow{v_2} = \overrightarrow{A_{p_{i+1}}A_{p_{i+2}}}$。如果将 $\overrightarrow{v_1}$ 逆时针旋转最小角度后与 $\overrightarrow{v_2}$ 方向一致，则称第 $i$ 次转弯为左转，否则为右转。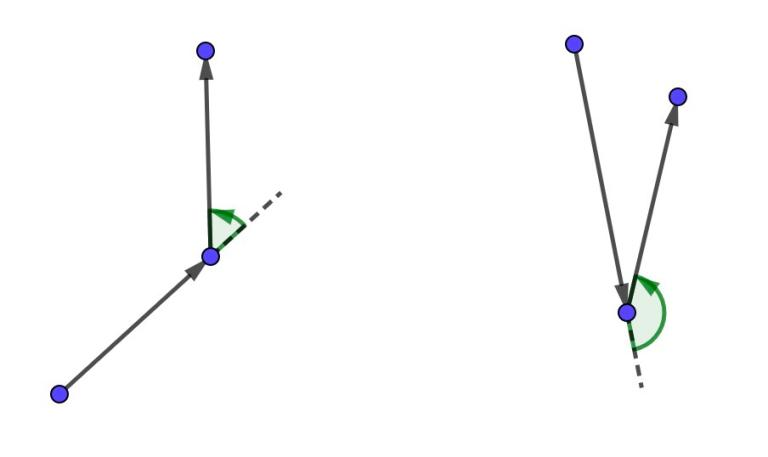为了更好地理解，请参考以下关于转弯的示意图：  上图为左转示例。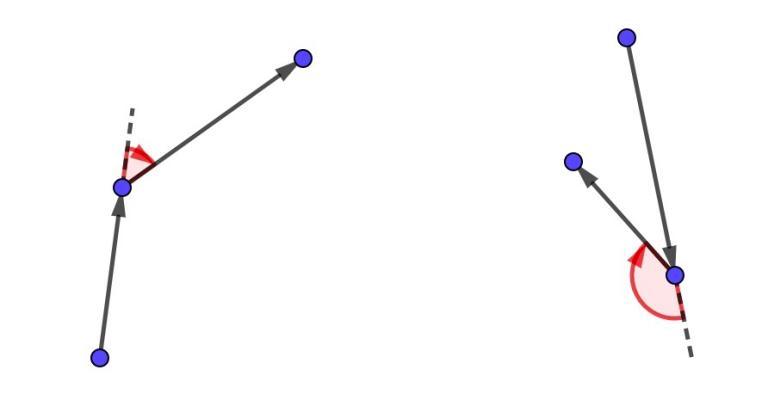  上图为右转示例。 现在给定 $A_1, A_2, \ldots, A_n$ 的坐标和字符串 $s$，请你找到一个 $1$ 到 $n$ 的排列 $p_1, p_2, \ldots, p_n$，使得 Vasya 画出的折线满足上述两个条件。

第一行包含一个整数 $n$，表示点的数量（$3 \leq n \leq 2000$）。 接下来的 $n$ 行，每行包含两个用空格分隔的整数 $x_i$ 和 $y_i$，表示点 $A_i$ 的坐标（$-10^9 \leq x_i, y_i \leq 10^9$）。 最后一行包含一个长度为 $n-2$ 的字符串 $s$，由字母 "L" 和 "R" 组成。 保证所有点均不同，且任意三点不共线。

如果不存在满足条件的排列，输出 $-1$。 否则，输出 $n$ 个数 $p_1, p_2, \ldots, p_n$，表示找到的排列（$1 \leq p_i \leq n$，且 $p_1, p_2, \ldots, p_n$ 互不相同）。如果有多组解，输出任意一组均可。

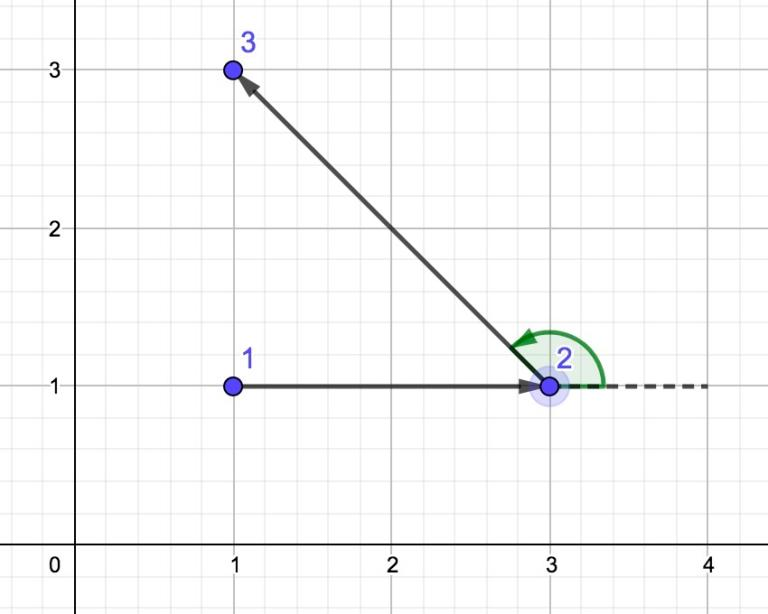
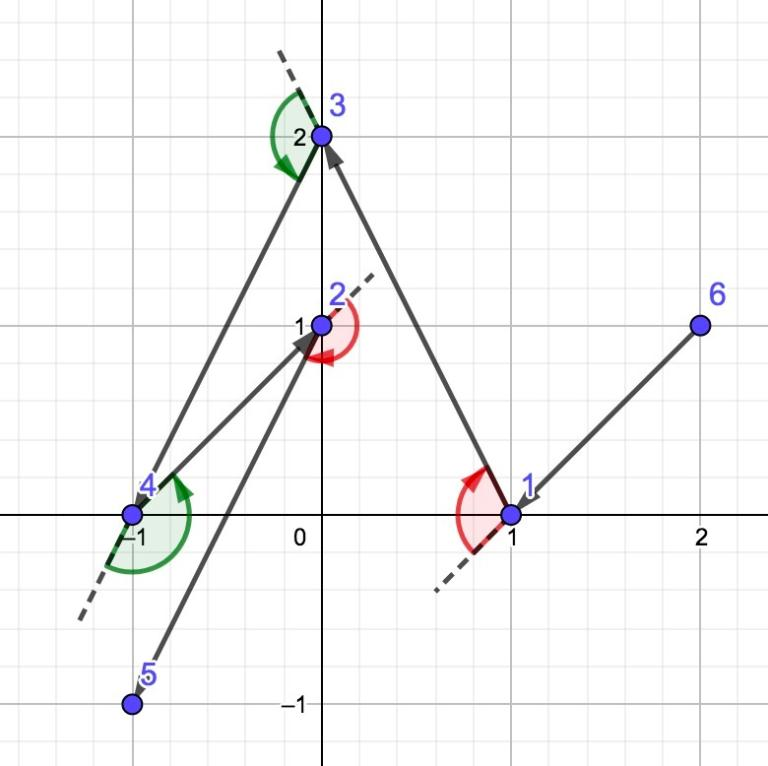
下图为第 1 组样例的折线：  可以看到，这条折线不自交且为绕行折线，因为在点 $2$ 处为左转。 下图为第 2 组样例的折线：  由 ChatGPT 4.1 翻译