CF115C Plumber

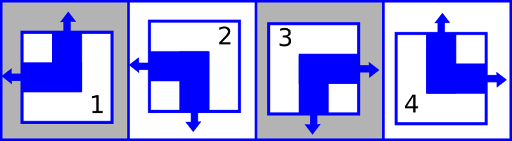
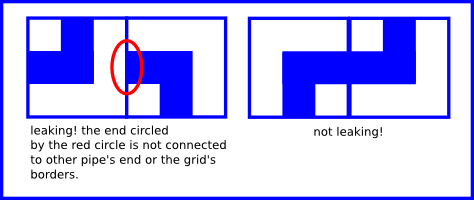
小约翰励志成为一名管道工！今天他画了一个包含 $n$ 行 $m$ 列的网格。 在每个单元格中，他将画一段管道。他只能画四种部分管道，使用 1 至 4 标号，如图。  每一个管道都有两端，在上图中使用箭头表示。例如，第 1 幅图的管道的两端分别在上面和左面， 如果网格内有部分管道的末端未连接到另一个管道的末端或网格的边界，则小约翰认为管道系统存在漏洞。下面这幅图就展示了一个在 $1 \times 2$ 的管道组中一个有漏洞的连接和没有漏洞的连接。  现在给你一个小约翰已经完成部分的管道组。每一个网格中要么有按要求填充的管道，要么没有被填充。您需要找出可组成多少个没有漏洞的管道。将结果取余 $10^6 +3$。 需要注意的是，网格不允许旋转或翻转。因此仅当其中之一水平或垂直旋转或翻转时才相同的两个配置被视为两种不同的方法。

第一行输入 $n$，$m$（$1

输出最多能有多少种无漏洞的的管道。如果没有，输出 0；否则，将答案取余 $10^6 + 3$

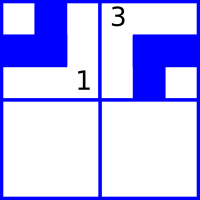
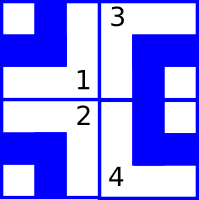
##### 样例 1 解释 网格初始配置如图。  所以最终无漏洞配置只有两种，如下图。   ##### 样例 2 解释 小约翰已完成的管道已经有漏洞了，所以无法拼成无漏洞的管道组。 ##### 样例 3 解释 只有一种方法，如图。  **严格遵照原文，未加改动** 翻译者：[瀛洲仙子](https://www.luogu.com.cn/user/517637)，[郭梁](https://www.luogu.com.cn/user/284186) 提交者：[瀛洲仙子](https://www.luogu.com.cn/user/517637)