CF1163F Indecisive Taxi Fee

在 Kuro 和 Shiro 居住的 Capypaland 城市中，有 $n$ 个城镇，编号从 $1$ 到 $n$，并有 $m$ 条双向道路，编号从 $1$ 到 $m$，连接着这些城镇。第 $i$ 条道路连接城镇 $u_i$ 和 $v_i$。由于城镇之间出行较为困难，出租车行业在这里非常流行。为了在激烈的竞争中生存下去，每家出租车公司都需要为顾客提供独特的服务。 Kuro 是一家出租车公司的老板。他决定为自己的出租车品牌引入一种新的计费模式，每次乘车的费用不再按路程长度计算，而是按所经过道路的价格之和来计算。每条道路 $i$ 的价格为 $w_i$，因此一次乘车经过道路 $e_1, e_2, \ldots, e_k$ 的费用为 $\sum_{i=1}^k w_{e_i}$。 然而，Kuro 本人是个优柔寡断的人，所以他拟定了 $q$ 个更改道路价格的方案。每个方案都基于原始价格 $w_i$，但会将某一条道路 $t_j$ 的价格更改为 $x_j$。注意，这些方案彼此独立。 Shiro 是 Kuro 出租车品牌的常客，因为她每天都要从城镇 $1$ 前往城镇 $n$。由于她是如此的常客，Kuro 决定在公开这些方案前，先将所有 $q$ 个方案展示给她。现在，Shiro 想知道，在每个方案下，她从城镇 $1$ 到城镇 $n$ 所需支付的最低费用是多少。

第一行包含三个整数 $n$、$m$ 和 $q$（$2 \le n \le 2 \cdot 10^5$，$1 \le m, q \le 2 \cdot 10^5$）——城镇数、道路数和 Kuro 拟定的方案数。 接下来的 $m$ 行中，第 $i$ 行包含三个整数 $u_i$、$v_i$ 和 $w_i$（$1 \le u_i, v_i \le n$，$1 \le w_i \le 10^9$，$u_i \ne v_i$）——表示第 $i$ 条道路连接的两个端点及其原始价格。 保证至少存在一条从城镇 $1$ 到城镇 $n$ 的路径。 接下来的 $q$ 行中，每行包含两个整数 $t_j$ 和 $x_j$（$1 \leq t_j \leq m, 1 \leq x_j \leq 10^9$）——表示 Kuro 计划更改的道路编号及其新价格。

输出 $q$ 个整数，第 $i$ 个整数表示在第 $i$ 个方案下，Shiro 从城镇 $1$ 到城镇 $n$ 所需支付的最低费用。

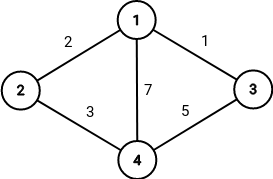
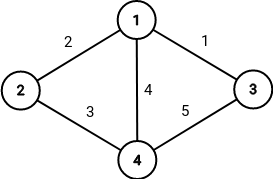
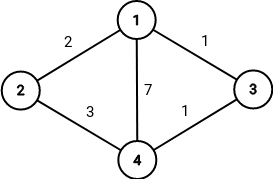
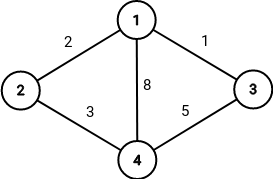
在第一个样例中，Capypaland 的原始示意图如下，每条道路旁的数字表示该道路的原始价格：  第一个方案的示意图如下：  在该方案下，Shiro 需支付的最低费用为 $4$，对应路径为 $1 \rightarrow 4$。 第二个方案的示意图如下：  在该方案下，Shiro 需支付的最低费用为 $2$，对应路径为 $1 \rightarrow 3 \rightarrow 4$。 第三个方案的示意图如下：  在该方案下，Shiro 需支付的最低费用为 $5$，对应路径为 $1 \rightarrow 2 \rightarrow 4$。 由 ChatGPT 4.1 翻译