CF1167G Low Budget Inception

我们渐感无趣，并打算猜测在超低预算下，影片会如何进行「开头」的制作。 我们仍记得的第一个场景中，整个城市都扭曲了：  它或许需要很高的 CGI 费用，但幸运地，我们有另一个类似的廉价方案。 首先，忘却一切的 3D，那些只是土豪的玩具！ 现在，城市以一条数轴表示。 第二，这个城市没有必要符合常理。 数轴上有 $n$ 个建筑物，建筑物都可以视作 $1 \times 1$ 的正方形。 **建筑物按其位置的升序，依次编号为 $1,\dots,n$。** 第 $i$ 个建筑物的左下角和右下角分别位于 $a_i$ 和 $a_i + 1$ 处。 并且，保证相邻建筑物的距离不超过 $d$（单纯为了让城市看上去不那么稀疏）。 其中第 $i$ 个和第 $i + 1$ 个建筑物的距离为前者的右下角和后者的左下角的距离。 最后，曲率也非常难以复现。 我们使用如下算法来处理整点 $x$ 处的弯曲： 令一条从 $x$ 向 $+\infty$ 延伸的射线及其经过的所有建筑物绕点 $x$ 开始逆时针转动。直到某个角度，一些建筑物将会触及其他建筑物或者数轴的一部分。 这个角度就是弯曲的结果。 （建筑物被破坏也不会花费额外经费） **最终状态下，我们称两条射线之间的角度为最终角度 $\alpha_x$。** 最后的问题在于寻找最佳的 $x$ 并进行弯曲。幸运的是，我们已经有了 $m$ 个候选点。 于是，你的任务是帮助我们对于候选点中的所有 $x$，计算所有的最终角度 $\alpha_x$。

第一行，两个整数 $n,d\;(1 \le n \le 2 \cdot 10^5,0 \le d \le 7000)$，表示建筑物的个数和相邻建筑物的最大距离。 第二行，$n$ 个整数 $a_1,\dots,a_n\;(a_1 = 0,0 < a_{i + 1} - a_i \le d + 1)$，表示建筑物的坐标。 第三行，一个整数 $m\;(1 \le m \le 2 \cdot 10^5)$，表示候选点的个数。 第四行，$m$ 个整数 $x_1,\dots,x_m\;(0 \le x_i \le a_n + 1,x_i < x_{i + 1})$，表示候选点的坐标。

对于每个 $x_i$，输出 $\alpha_{x_i}$（以弧度表示）。 误差不超过 $10^{-9}$。

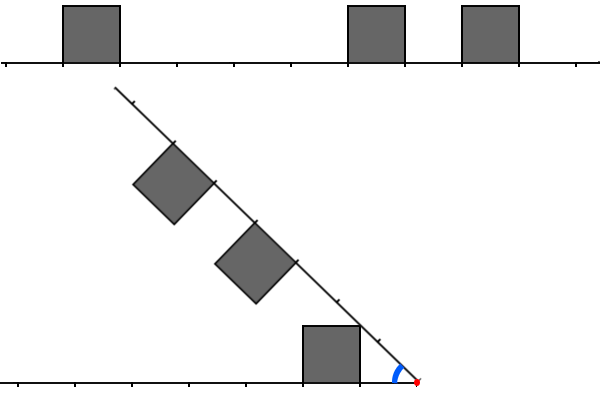
你可以在此看见第一个样例中的城市和 $2$ 处的弯曲。你需要测量的角度已经被标记为蓝色。它等于 $\frac \pi 4$。 没有任何一对建筑物的距离超过 $4$，所以当 $d = 4$ 时也合法。