CF1172B Nauuo and Circle
题目描述
给定一圆,上有n个节点(不重合,从1到n编号)。它们按照输入连成一棵树。
求合法树的方案总数,对998244353取模。
一棵树是合法的,当且仅当这棵树中无交叉的边(两边共用一端点除外)。
注意:只要从 **最上面端点(不一定对于每个都是1,见样例1解释3&5)** 顺时针沿圆遍历所有节点得到的序列不同,那么两种方案就是不同的,即使它们本质相同。
输入格式
The first line contains a single integer $ n $ ( $ 2\le n\le 2\cdot 10^5 $ ) — the number of nodes in the tree.
Each of the next $ n-1 $ lines contains two integers $ u $ and $ v $ ( $ 1\le u,v\le n $ ), denoting there is an edge between $ u $ and $ v $ .
It is guaranteed that the given edges form a tree.
输出格式
The output contains a single integer — the number of permutations suitable to draw the given tree on a circle satisfying the rule, modulo $ 998244353 $ .
说明/提示
Example 1
All valid permutations and their spanning trees are as follows.
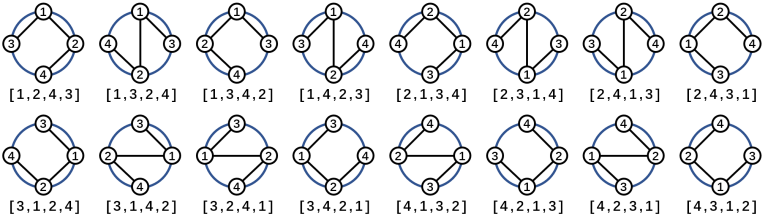
Here is an example of invalid permutation: the edges $ (1,3) $ and $ (2,4) $ are crossed.
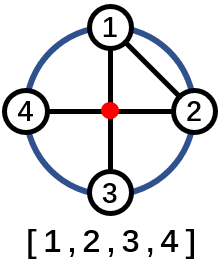
Example 2
Every permutation leads to a valid tree, so the answer is $ 4! = 24 $ .