CF1172D Nauuo and Portals

Nauuo 是一个喜欢玩与传送门相关游戏的女孩。 有一天，她玩了这样一个游戏。 在一个 $n\times n$ 的网格中，行从上到下编号为 $1$ 到 $n$，列从左到右编号为 $1$ 到 $n$。我们用 $(r,c)$ 表示第 $r$ 行第 $c$ 列的格子。 一个传送门由一对门组成。你可以从其中一扇门传送到另一扇门，并且不会改变你的前进方向。更正式地说，如果你走进一个有门的格子，你会被传送到同一传送门的另一扇门所在的格子，然后继续以原来的方向进入下一个格子。一个格子里不能有多于一扇门。 “下一个格子”指的是你面朝的方向上最近的格子。例如，如果你面朝下方，$(2,5)$ 的下一个格子是 $(3,5)$。 如果你走进一个没有门的格子，你必须继续以当前方向进入下一个格子。如果下一个格子不存在，你就会离开网格。 你需要在网格中设置一些（可能为零）传送门，使得：如果你从 $(i,1)$ 面朝右进入，你最终会从 $(r_i,n)$ 离开网格；如果你从 $(1,i)$ 面朝下进入，你会从 $(n,c_i)$ 离开网格。 保证 $r_{1..n}$ 和 $c_{1..n}$ 都是 $n$ 的一个排列。$n$ 的一个排列是一个长度为 $n$ 的数列 $p_1,p_2,\ldots,p_n$，其中每个 $1$ 到 $n$ 的整数恰好出现一次。 她在玩游戏时感到困惑，你能帮她找到一种方案吗？

第一行包含一个整数 $n$（$1\le n\le 1000$）——网格的边长。 第二行包含 $n$ 个整数 $r_1,r_2,\ldots,r_n$（$1\le r_i\le n$）——如果你从 $(i,1)$ 面朝右进入，你应当从 $(r_i,n)$ 离开网格。保证 $r_{1..n}$ 是 $n$ 的一个排列。 第三行包含 $n$ 个整数 $c_1,c_2,\ldots,c_n$（$1\le c_i\le n$）——如果你从 $(1,i)$ 面朝下进入，你应当从 $(n,c_i)$ 离开网格。保证 $c_{1..n}$ 是 $n$ 的一个排列。

如果无法满足要求，输出唯一的数字 $-1$。 否则，第一行输出一个整数 $m$（$0\le m\le\frac{n^2}{2}$）——你设置的传送门数量。 接下来的 $m$ 行，每行四个整数 $x_1,y_1,x_2,y_2$，表示你在 $(x_1,y_1)$ 和 $(x_2,y_2)$ 设置了一对传送门。 如果有多种方案，输出任意一种即可。你不需要使 $m$ 最小。

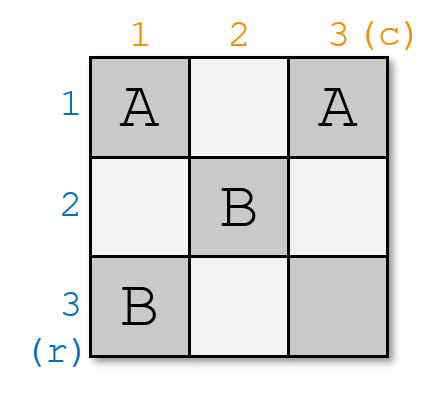
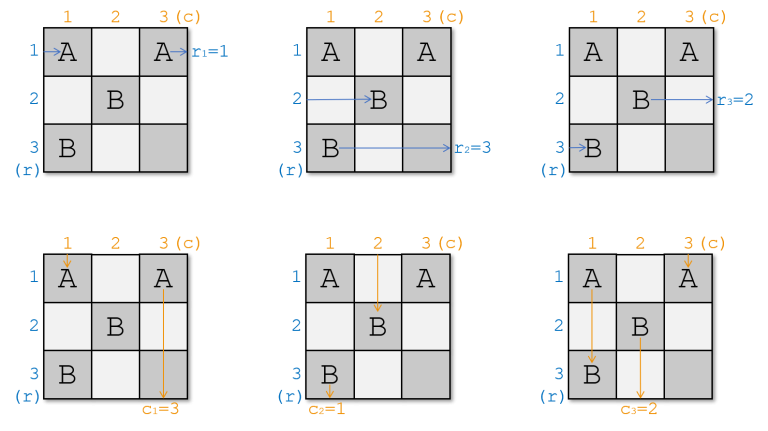
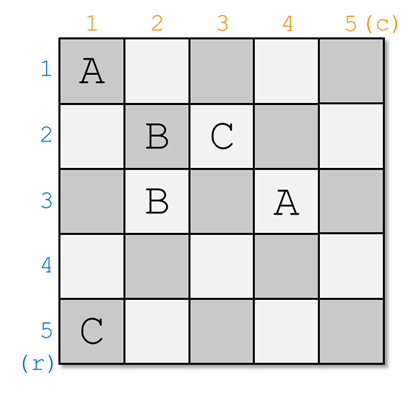
示例 1 带有相同字母的格子是一对传送门。你可以这样设置传送门：  它满足要求，因为：  示例 2 你可以这样设置传送门：  由 ChatGPT 4.1 翻译