CF1173B Nauuo and Chess

Nauuo is a girl who loves playing chess. One day she invented a game by herself which needs $ n $ chess pieces to play on a $ m\times m $ chessboard. The rows and columns are numbered from $ 1 $ to $ m $ . We denote a cell on the intersection of the $ r $ -th row and $ c $ -th column as $ (r,c) $ . The game's goal is to place $ n $ chess pieces numbered from $ 1 $ to $ n $ on the chessboard, the $ i $ -th piece lies on $ (r_i,\,c_i) $ , while the following rule is satisfied: for all pairs of pieces $ i $ and $ j $ , $ |r_i-r_j|+|c_i-c_j|\ge|i-j| $ . Here $ |x| $ means the absolute value of $ x $ . However, Nauuo discovered that sometimes she couldn't find a solution because the chessboard was too small. She wants to find the smallest chessboard on which she can put $ n $ pieces according to the rules. She also wonders how to place the pieces on such a chessboard. Can you help her?

The only line contains a single integer $ n $ ( $ 1\le n\le 1000 $ ) — the number of chess pieces for the game.

The first line contains a single integer — the minimum value of $ m $ , where $ m $ is the length of sides of the suitable chessboard. The $ i $ -th of the next $ n $ lines contains two integers $ r_i $ and $ c_i $ ( $ 1\le r_i,c_i\le m $ ) — the coordinates of the $ i $ -th chess piece. If there are multiple answers, print any.

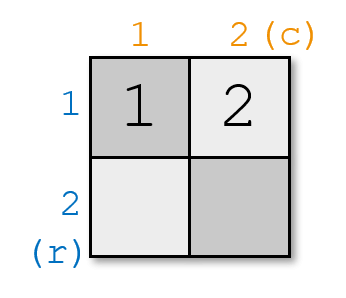
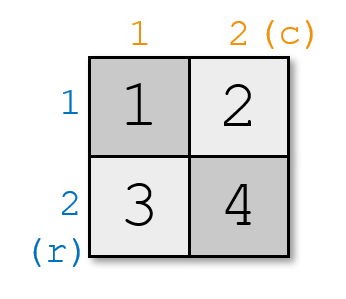
In the first example, you can't place the two pieces on a $ 1\times1 $ chessboard without breaking the rule. But you can place two pieces on a $ 2\times2 $ chessboard like this:  In the second example, you can't place four pieces on a $ 2\times2 $ chessboard without breaking the rule. For example, if you place the pieces like this:  then $ |r_1-r_3|+|c_1-c_3|=|1-2|+|1-1|=1 $ , $ |1-3|=2 $ , $ 1