CF1173B Nauuo and Chess

Nauuo 是一个喜欢下棋的女孩。 有一天，她自己发明了一种游戏，需要用 $n$ 个棋子在一个 $m\times m$ 的棋盘上进行。棋盘的行和列编号均从 $1$ 到 $m$。我们用 $(r, c)$ 表示第 $r$ 行第 $c$ 列的格子。 游戏的目标是将编号为 $1$ 到 $n$ 的 $n$ 个棋子放在棋盘上，第 $i$ 个棋子放在 $(r_i, c_i)$，同时满足以下规则：对于所有棋子对 $i$ 和 $j$，都有 $|r_i - r_j| + |c_i - c_j| \ge |i - j|$。其中 $|x|$ 表示 $x$ 的绝对值。 然而，Nauuo 发现有时候棋盘太小，她无法找到满足条件的方案。 她想知道，最小需要多大的棋盘，才能按照规则放下 $n$ 个棋子。 她还想知道，在这样最小的棋盘上，应该如何放置这些棋子。你能帮帮她吗？

一行一个整数 $n$（$1 \le n \le 1000$），表示游戏所需的棋子数量。

第一行输出一个整数，表示最小的 $m$，即满足条件的棋盘边长。 接下来 $n$ 行，每行两个整数 $r_i$ 和 $c_i$（$1 \le r_i, c_i \le m$），表示第 $i$ 个棋子的坐标。 如果有多组答案，输出任意一组均可。

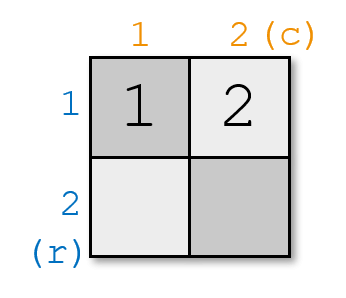
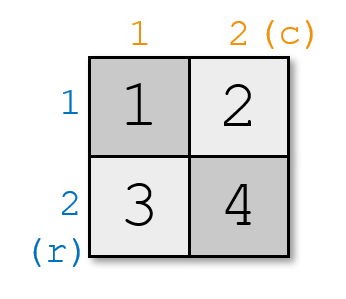
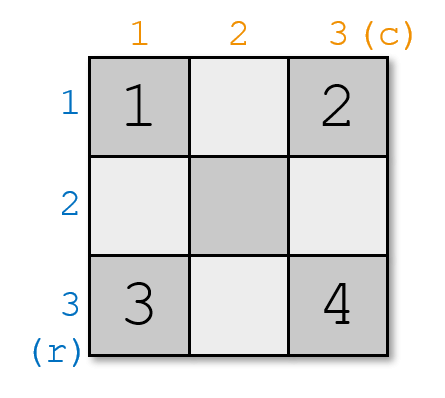
在第一个样例中，你无法在 $1\times1$ 的棋盘上放下两个棋子而不违反规则。但你可以在 $2\times2$ 的棋盘上这样放置两个棋子：  在第二个样例中，你无法在 $2\times2$ 的棋盘上放下四个棋子而不违反规则。例如，如果你这样放置棋子：  那么 $|r_1 - r_3| + |c_1 - c_3| = |1-2| + |1-1| = 1$，$|1-3| = 2$，$1 < 2$；并且 $|r_1 - r_4| + |c_1 - c_4| = |1-2| + |1-2| = 2$，$|1-4| = 3$，$2 < 3$。这不满足规则。 然而，在 $3\times3$ 的棋盘上，你可以这样放置四个棋子：  由 ChatGPT 4.1 翻译