CF1178D Prime Graph

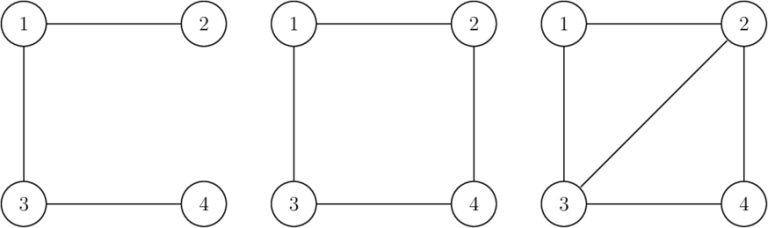
每个人都喜欢质数。Alice 是一个人，因此她也喜欢质数。Bob 想送她一份充满爱意的礼物，但他想不出什么新奇的东西。因此，他决定送她一张图。多么有创意啊，Bob！Alice 一定会很高兴！ 在构建这张图时，他需要满足以下四个条件： - 图必须是一个简单无向图，即没有重边和自环。 - 顶点数必须恰好为 $n$ —— 这是他选定的数字。这个数字不一定是质数。 - 总边数必须是质数。 - 每个顶点的度数（即与该顶点相连的边的数量）必须是质数。 下面是 $n=4$ 的一个例子。第一个图（左边）不合法，因为顶点 $2$（以及 $4$）的度数为 $1$，而 $1$ 不是质数。第二个图（中间）不合法，因为总边数为 $4$，不是质数。第三个图（右边）是一个合法的答案。  注意，图可以是不连通的。 请你帮助 Bob 找到任意一张满足条件的图！

输入包含一个整数 $n$（$3 \leq n \leq 1000$），表示顶点的数量。

如果不存在满足条件的图，输出一行 $-1$。 否则，首先输出一行一个质数 $m$（$2 \leq m \leq \frac{n(n-1)}{2}$），表示图中的边数。接下来输出 $m$ 行，每行两个整数 $u_i, v_i$（$1 \leq u_i, v_i \leq n$），表示在顶点 $u_i$ 和 $v_i$ 之间有一条边。每个顶点的度数必须是质数。图中不能有重边或自环。 如果有多组解，你可以输出任意一组。 注意，图可以是不连通的。

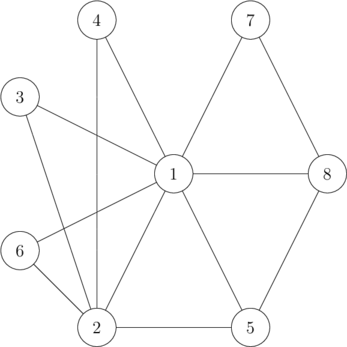
第一个样例在题目描述中已经给出。 在第二个样例中，各顶点的度数为 $[7, 5, 2, 2, 3, 2, 2, 3]$。这些数都是质数。此外，边数 $13$ 也是质数，因此都满足条件。  由 ChatGPT 4.1 翻译