CF1178F1 Short Colorful Strip

This is the first subtask of problem F. The only differences between this and the second subtask are the constraints on the value of $ m $ and the time limit. You need to solve both subtasks in order to hack this one. There are $ n+1 $ distinct colours in the universe, numbered $ 0 $ through $ n $ . There is a strip of paper $ m $ centimetres long initially painted with colour $ 0 $ . Alice took a brush and painted the strip using the following process. For each $ i $ from $ 1 $ to $ n $ , in this order, she picks two integers $ 0 \leq a_i < b_i \leq m $ , such that the segment $ [a_i, b_i] $ is currently painted with a single colour, and repaints it with colour $ i $ . Alice chose the segments in such a way that each centimetre is now painted in some colour other than $ 0 $ . Formally, the segment $ [i-1, i] $ is painted with colour $ c_i $ ( $ c_i \neq 0 $ ). Every colour other than $ 0 $ is visible on the strip. Count the number of different pairs of sequences $ \{a_i\}_{i=1}^n $ , $ \{b_i\}_{i=1}^n $ that result in this configuration. Since this number may be large, output it modulo $ 998244353 $ .

The first line contains a two integers $ n $ , $ m $ ( $ 1 \leq n \leq 500 $ , $ n = m $ ) — the number of colours excluding the colour $ 0 $ and the length of the paper, respectively. The second line contains $ m $ space separated integers $ c_1, c_2, \ldots, c_m $ ( $ 1 \leq c_i \leq n $ ) — the colour visible on the segment $ [i-1, i] $ after the process ends. It is guaranteed that for all $ j $ between $ 1 $ and $ n $ there is an index $ k $ such that $ c_k = j $ . Note that since in this subtask $ n = m $ , this means that $ c $ is a permutation of integers $ 1 $ through $ n $ .

Output a single integer — the number of ways Alice can perform the painting, modulo $ 998244353 $ .

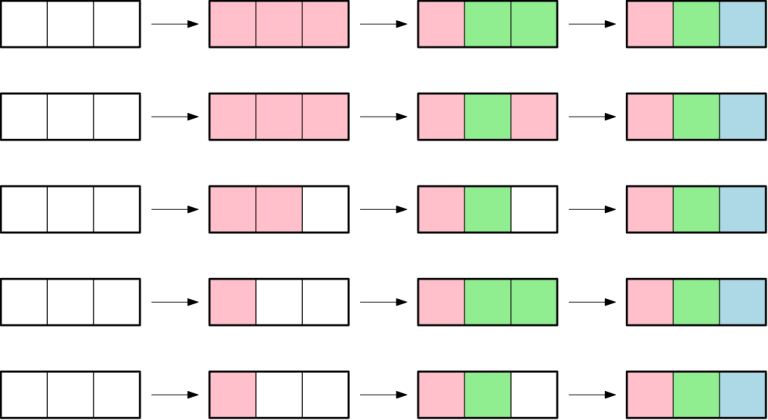
In the first example, there are $ 5 $ ways, all depicted in the figure below. Here, $ 0 $ is white, $ 1 $ is red, $ 2 $ is green and $ 3 $ is blue.  Below is an example of a painting process that is not valid, as in the second step the segment 1 3 is not single colour, and thus may not be repainted with colour $ 2 $ .