CF1178F2 Long Colorful Strip

这是 F 题的第二个子任务。F1 和 F2 的区别仅在对于 $m$ 和时间的限制上 有 $n+1$ 种颜色标号从 $0$ 到 $n$，我们有一条全部染成颜色 $0$ 的长为 $m$ 的纸带。 Alice 拿着刷子通过以下的过程来给纸带染色： 我们按照从 $1$ 到 $n$ 的顺序进行染色，进行每次染色时，我们选取一个区间 $[a_i,b_i]$，$0 \le a_i < b_i \le m$，并且这个区间内必定是单种颜色。 染色到最后，纸带上有各种颜色除了颜色 $0$。给出纸带最终的状态，问有多少种不同的染色方案能到达最终状态。输出时结果模 $998244353$。

第一行有两个整数 $n$ 和 $m$，$1 \le n \le 500$，$n \le m \le 10^6$。$n$ 代表除了颜色 $0$ 有多少种颜色，$m$ 代表纸带的长度。 第二行有 $m$ 个用空格分隔的整数 $c_1,c_2,\dots,c_m$，$1

输入一个单独的整数，即 Alice 可行的染色方案数模 $998244353$。

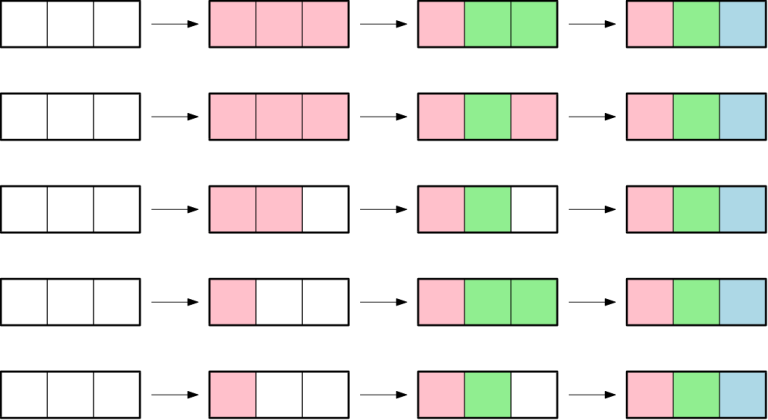
In the first example, there are $ 5 $ ways, all depicted in the figure below. Here, $ 0 $ is white, $ 1 $ is red, $ 2 $ is green and $ 3 $ is blue.  Below is an example of a painting process that is not valid, as in the second step the segment 1 3 is not single colour, and thus may not be repainted with colour $ 2 $ .  In the second example, Alice must first paint segment 0 3 with colour $ 1 $ and then segment 1 2 with colour $ 2 $ .