CF117E Tree or not Tree

You are given an undirected connected graph $ G $ consisting of $ n $ vertexes and $ n $ edges. $ G $ contains no self-loops or multiple edges. Let each edge has two states: on and off. Initially all edges are switched off. You are also given $ m $ queries represented as $ (v,u) $ — change the state of all edges on the shortest path from vertex $ v $ to vertex $ u $ in graph $ G $ . If there are several such paths, the lexicographically minimal one is chosen. More formally, let us consider all shortest paths from vertex $ v $ to vertex $ u $ as the sequences of vertexes $ v,v_{1},v_{2},...,u $ . Among such sequences we choose the lexicographically minimal one. After each query you should tell how many connected components has the graph whose vertexes coincide with the vertexes of graph $ G $ and edges coincide with the switched on edges of graph $ G $ .

The first line contains two integers $ n $ and $ m $ ( $ 3

Print $ m $ lines, each containing one integer — the query results.

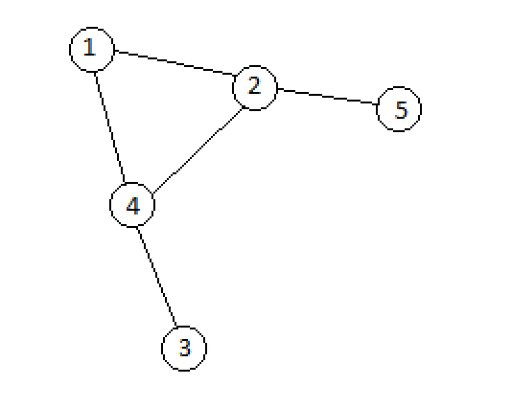
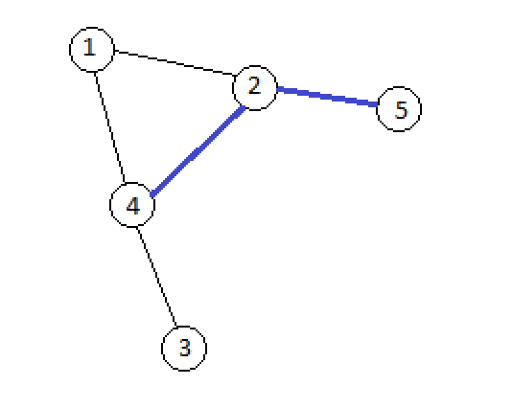
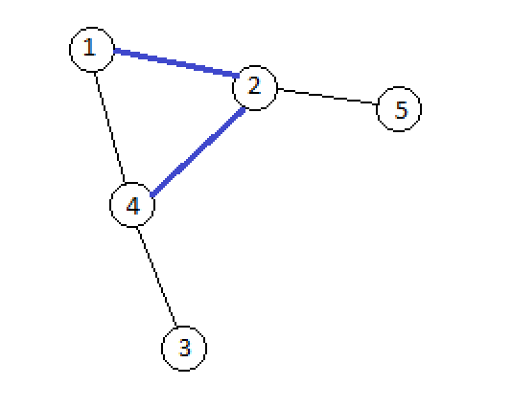
Let's consider the first sample. We'll highlight the switched on edges blue on the image. - The graph before applying any operations. No graph edges are switched on, that's why there initially are 5 connected components.  - The graph after query $ v=5,u=4 $ . We can see that the graph has three components if we only consider the switched on edges.  - The graph after query $ v=1,u=5 $ . We can see that the graph has three components if we only consider the switched on edges.  Lexicographical comparison of two sequences of equal length of $ k $ numbers should be done as follows. Sequence $ x $ is lexicographically less than sequence $ y $ if exists such $ i $ ( $ 1