CF117E Tree or not Tree
题目描述
给定一个无向连通图 $G$,包含 $n$ 个顶点和 $n$ 条边。$G$ 中没有自环或重边。每条边有两种状态:开(on)和关(off)。初始时所有边都处于关闭状态。
你还会得到 $m$ 个查询,每个查询为 $(v,u)$ ——将图 $G$ 中从顶点 $v$ 到顶点 $u$ 的最短路径上的所有边的状态取反。如果存在多条最短路径,则选择字典序最小的那一条。更正式地说,设从顶点 $v$ 到顶点 $u$ 的所有最短路径为顶点序列 $v,v_{1},v_{2},...,u$,在这些序列中选择字典序最小的那一条。
每次查询后,你需要输出仅考虑当前已打开的边时,图 $G$ 的连通分量个数。
输入格式
第一行包含两个整数 $n$ 和 $m$($3 \leq n \leq 10^{5}$,$1 \leq m \leq 10^{5}$)。接下来的 $n$ 行描述图的边,每行两个整数 $a$ $b$($1 \leq a,b \leq n$)。接下来的 $m$ 行,每行两个整数 $v$ $u$($1 \leq v,u \leq n$),表示一个查询。
保证图是连通的,没有自环或重边。
输出格式
输出 $m$ 行,每行一个整数,表示每次查询后的连通分量个数。
说明/提示
我们来看第一个样例。我们将在图片中用蓝色高亮表示已打开的边。
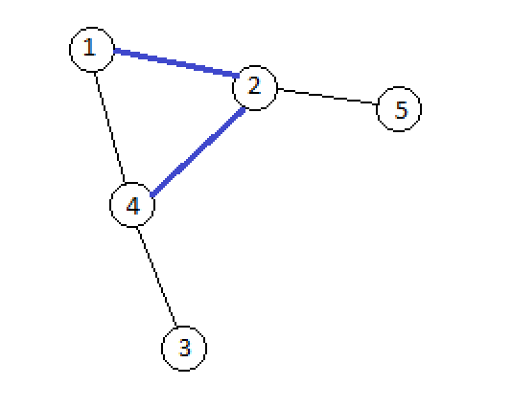
- 在执行任何操作前,图中没有任何边被打开,因此初始时有 5 个连通分量。
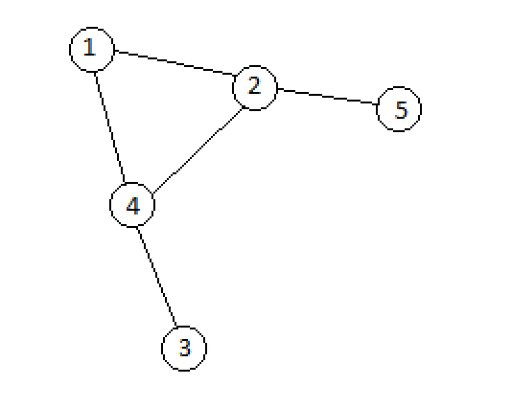
- 执行查询 $v=5,u=4$ 后,仅考虑已打开的边,图中有 3 个连通分量。
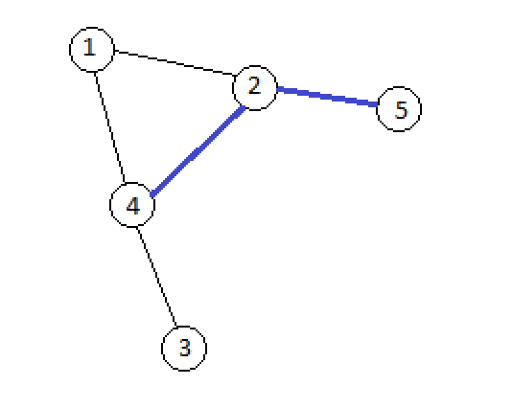
- 执行查询 $v=1,u=5$ 后,仅考虑已打开的边,图中有 3 个连通分量。
对于长度相等的两个数列 $k$,字典序比较方式如下:若存在某个 $i$($1 \leq i \leq k$),使得 $x_{i} < y_{i}$,且对于所有 $j$($1 \leq j < i$)都有 $x_{j} = y_{j}$,则序列 $x$ 的字典序小于序列 $y$。
由 ChatGPT 4.1 翻译