CF1184C3 Heidi and the Turing Test (Hard)

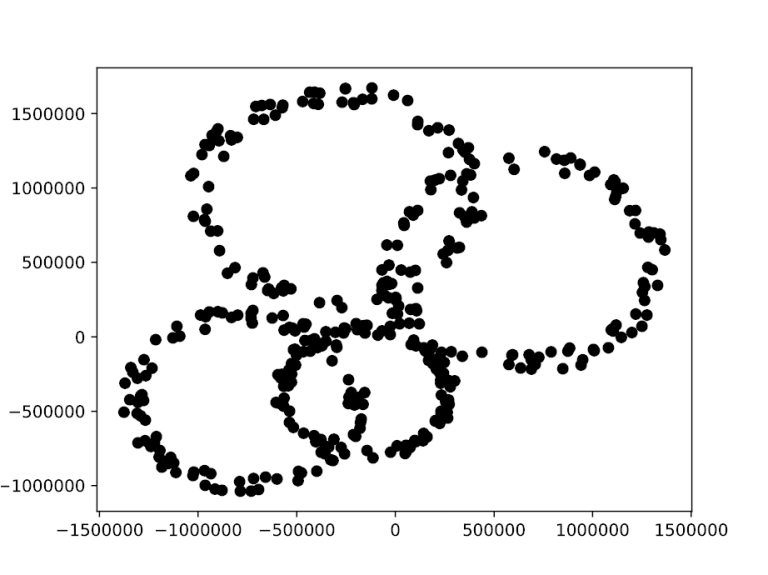
赛博人再次智胜了戴立克！不幸的是，这一次戴立克决定彻底放弃这些任务，这意味着博士不得不亲自应对他们。 博士可以独自对付戴立克，但现在 Heidi 必须确保赛博人忙于下一个任务。 平面上有 $k$ 个圆环。对于每个圆环，均匀采样 $n$ 个点，并加入微小的随机噪声。任务是仅根据这些带噪声的采样点，恢复出这些圆环。 圆环和采样点的生成方式如下：圆环的圆心从以原点为中心、半径为 $1\,000\,000$ 的圆盘内均匀采样，圆环的半径从区间 $[250\,000, 750\,000]$ 内均匀采样。设 $R$ 为圆心为 $(x, y)$、半径为 $r$ 的圆环。采样点的生成方式为：从区间 $[0, 2\pi]$ 内均匀采样一个角度 $\theta$，从区间 $[0.9r, 1.1r]$ 内均匀采样一个距离 $d$。采样点的坐标为 $(x+d\cos(\theta),\ y+d\sin(\theta))$，并四舍五入到最接近的整数。 圆环之间的距离用 Hausdorff 距离来度量。在本题中，两个圆环 $R_1, R_2$ 的距离定义如下。设 $d$ 为两个圆心之间的距离，$r_1, r_2$ 分别为半径，则距离为 $$ \text{dist}(R_1, R_2) = \max\big(\min(d_{--}, d_{-+}),\ \min(d_{+-}, d_{++}),\ \min(d_{--}, d_{+-}),\ \min(d_{-+}, d_{++})\big) $$ 其中 $d_{++} = |d + r_1 + r_2|$， $d_{+-} = |d + r_1 - r_2|$， $d_{-+} = |d - r_1 + r_2|$， $d_{--} = |d - r_1 - r_2|$。 如果输出的某个圆环与原始圆环 $R_0$ 的 Hausdorff 距离小于 $100\,000$，则称 $R_0$ 被恢复。 当所有圆环都被恢复时，输出才被接受。保证任意两个圆环之间的距离大于 $600\,000$。 请注意，人类可以非常容易地解决这个任务，所以请确保没有人类叛徒帮助赛博人完成这个任务。

第一行包含一个整数 $k$（$1 \leq k \leq 4$），表示圆环的数量。 第二行包含一个整数 $n$（$100 \leq n \leq 1\,000$），表示每个圆环采样的点数。 接下来的 $n \times k$ 行，每行包含两个整数 $x_i, y_i$，表示第 $i$ 个采样点的坐标。

（无输出格式说明，需根据题意自行推断。）

以下是 $k=4$ 且 $n=100$ 的测试用例示意图：  你可以在[这里](//assets.codeforces.com/rounds/1184/c1.zip)下载样例输入和输出。 由 ChatGPT 4.1 翻译