CF1187E Tree Painting

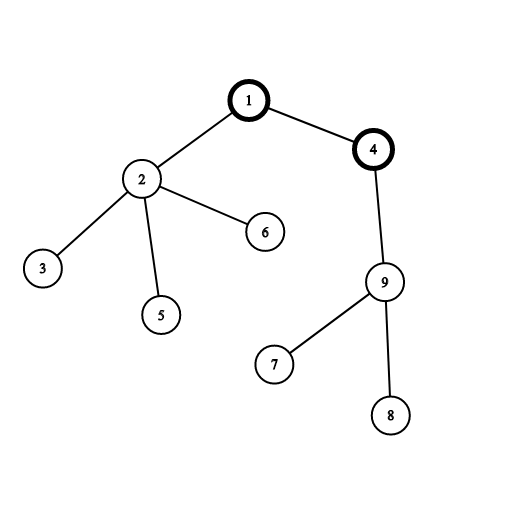
给定一棵包含 $n$ 个顶点的树（无向连通无环图）。你要在这棵树上玩一个游戏。 最开始所有顶点都是白色的。在游戏的第一回合，你选择一个顶点并将其染成黑色。之后的每一回合，你都可以选择一个与任意黑色顶点相邻的白色顶点，并将其染成黑色。 每当你选择一个顶点（包括第一回合），你获得的分数等于包含该顶点的、仅由白色顶点组成的连通块的大小。游戏在所有顶点都被染成黑色时结束。 来看下面这个例子：  顶点 $1$ 和 $4$ 已经被染成黑色。如果你选择顶点 $2$，你将获得 $4$ 分，因为包含顶点 $2, 3, 5, 6$ 的连通块的大小为 $4$。如果你选择顶点 $9$，你将获得 $3$ 分，因为包含顶点 $7, 8, 9$ 的连通块的大小为 $3$。 你的任务是最大化你获得的分数。

第一行包含一个整数 $n$，表示树的顶点数（$2 \le n \le 2 \times 10^5$）。 接下来的 $n-1$ 行，每行描述树的一条边。第 $i$ 条边由两个整数 $u_i$ 和 $v_i$ 表示，表示该边连接顶点 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n$，$u_i \ne v_i$）。 保证给定的边构成一棵树。

输出一个整数，表示如果你采取最优策略，最多可以获得多少分。

第一个示例的树如题目描述中的图片所示。 由 ChatGPT 4.1 翻译