CF1188A2 Add on a Tree: Revolution

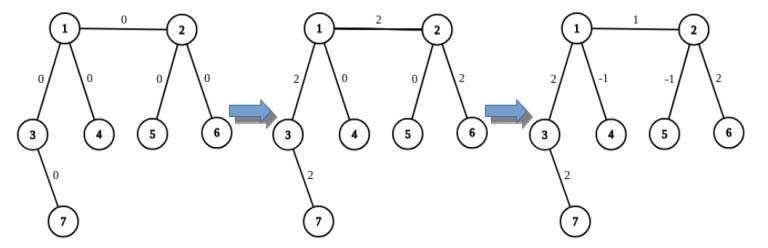
注意，这是两个类似问题中的第二个。如果你解决了本题，可以对本题进行 hack。但只有在你同时解决了这两个问题后，才能对前一个问题进行 hack。 给定一棵有 $n$ 个节点的树。初始时，所有边上的权值均为 $0$。每次操作，你可以选择任意两个不同的叶子节点 $u$、$v$，以及任意一个整数 $x$，然后将 $x$ 加到从 $u$ 到 $v$ 的简单路径上的所有边的权值上。注意，在前一个子任务中，$x$ 可以是任意实数，而在本题中，$x$ 必须是整数。 例如，下图展示了对图进行两次操作后的结果：先将 $2$ 加到从 $7$ 到 $6$ 的路径上，然后将 $-1$ 加到从 $4$ 到 $5$ 的路径上。  现在给定一组非负的、两两不同的偶数，分别写在每条边上。对于给定的配置，判断是否可以通过上述操作得到。如果可以，请输出一组操作序列，使得最终得到该配置。操作的限制条件见输出格式部分。 叶子节点是指度为 $1$ 的节点。简单路径是指不包含重复节点的路径。

第一行包含一个整数 $n$（$2 \le n \le 1000$），表示树的节点数。 接下来的 $n-1$ 行，每行包含三个整数 $u$、$v$、$val$（$1 \le u, v \le n$，$u \neq v$，$0 \le val \le 10\,000$），表示节点 $u$ 和 $v$ 之间有一条边，权值为 $val$。保证这些边构成一棵树。保证所有 $val$ 两两不同且为偶数。

如果不存在任何操作序列能够得到给定的配置，输出 “NO”。 如果存在，第一行输出 “YES”。第二行输出 $m$，表示你将要执行的操作次数（$0 \le m \le 10^5$）。注意，你不需要使操作次数最小！ 接下来 $m$ 行，每行输出一次操作，格式为： $u, v, x$（$1 \le u, v \le n$，$u \neq v$，$x$ 为整数，$-10^9 \le x \le 10^9$），其中 $u, v$ 为叶子节点，$x$ 为你要加的数。 保证如果存在能够得到给定配置的操作序列，则一定存在满足所有条件的操作序列。

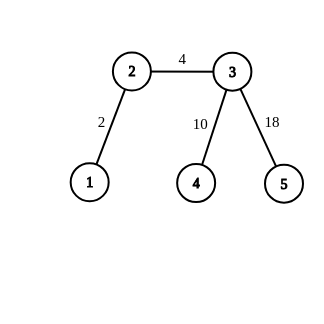
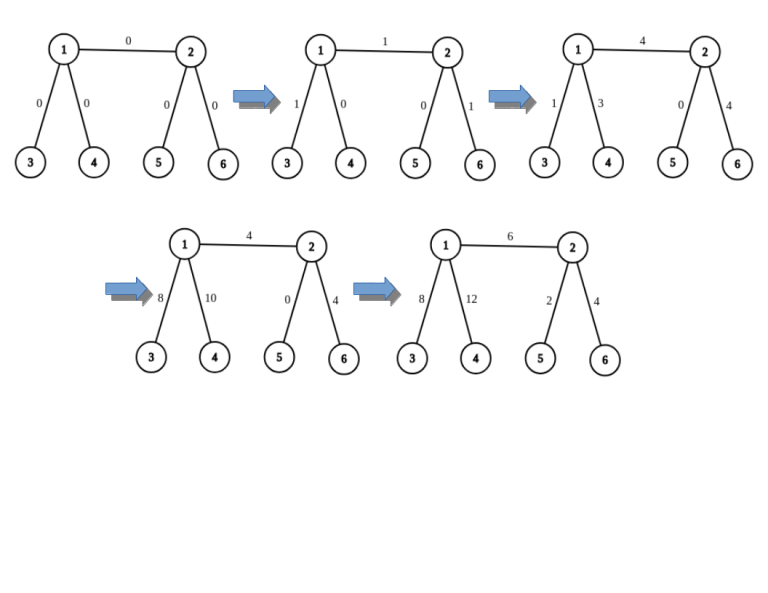
第一个样例中的配置如下图所示，不可能通过操作得到。  第二个样例的操作序列如下图所示。  由 ChatGPT 4.1 翻译