CF1189B Number Circle

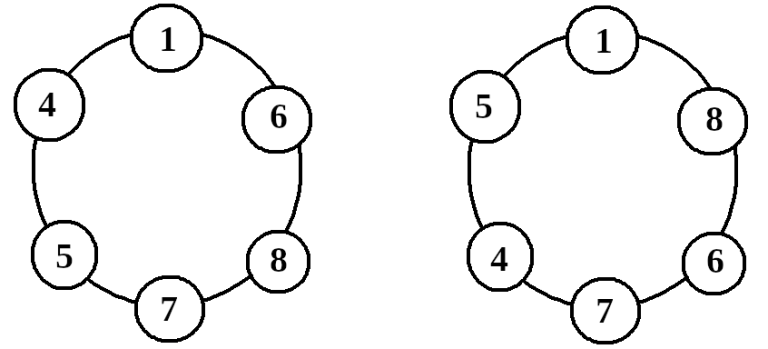
给定 $n$ 个数 $a_1, a_2, \ldots, a_n$，你能否将它们排成一个环，使得每个数都严格小于它相邻两个数之和？ 例如，对于数组 $[1, 4, 5, 6, 7, 8]$，左图的排列是合法的，而右图的排列不合法，因为 $5 \ge 4 + 1$ 且 $8 > 1 + 6$。 

第一行包含一个整数 $n$（$3 \le n \le 10^5$），表示数字的个数。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \leq a_i \le 10^9$），表示这些数。给定的数不一定各不相同（即允许有重复）。

如果无解，第一行输出 "NO"。 如果有解，第一行输出 "YES"。第二行输出 $n$ 个数，表示数组在环中的排列顺序。你输出的第一个和最后一个元素在环中视为相邻。如果有多种方案，输出任意一种即可。你可以从任意一个元素开始输出环。

第一组样例中一种可能的排列如下： $4 < 2 + 3$； $2 < 4 + 3$； $3 < 4 + 2$。 第二组样例中也有一种可能的排列。 在第三组样例中，无论如何排列 $13, 8, 5$，$13$ 的相邻数都是 $8$ 和 $5$，但 $13 \ge 8 + 5$。 第四组样例无解。 由 ChatGPT 4.1 翻译