CF1190D Tokitsukaze and Strange Rectangle

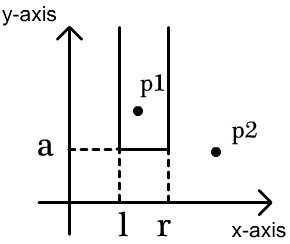
在平面上有 $n$ 个点，第 $i$ 个点的坐标为 $(x_i, y_i)$。Tokitsukaze 想要画出一个奇特的矩形区域，并选取该区域内的所有点。 这个奇特的区域由三条直线 $x = l$、$y = a$ 和 $x = r$ 所围成，分别作为左边界、下边界和右边界，其中 $l$、$r$ 和 $a$ 可以是任意实数，且满足 $l < r$。该区域的上边界是无界的，可以认为是一条在无穷远处与 $x$ 轴平行的直线。下图展示了一个奇特的矩形区域。  当且仅当 $l < x_i < r$ 且 $y_i > a$ 时，点 $(x_i, y_i)$ 在这个奇特的矩形区域内。例如，在上图中，$p_1$ 在区域内，而 $p_2$ 不在区域内。 Tokitsukaze 想知道，通过选取奇特矩形区域内的所有点，她最多能获得多少个不同的非空点集。我们认为如果存在至少一个点只属于其中一个集合而不属于另一个集合，则这两个集合不同。

第一行包含一个整数 $n$（$1 \leq n \leq 2 \times 10^5$），表示平面上的点的数量。 接下来的 $n$ 行，每行包含两个整数 $x_i, y_i$（$1 \leq x_i, y_i \leq 10^9$），表示第 $i$ 个点的坐标。 所有点的坐标均不相同。

输出一个整数，表示她能获得的不同非空点集的数量。

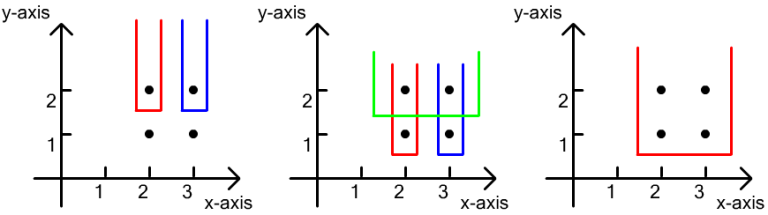
对于第一个样例，每个 $k = 1, 2, 3$ 都恰好有一个包含 $k$ 个点的集合，所以总数为 $3$。 对于第二个样例，分别有 $3$ 个只包含一个点的集合，$2$ 个包含两个点的集合，$1$ 个包含三个点的集合，总和为 $6$。 对于第三个样例，如下图所示： - 有 $2$ 个只包含一个点的集合； - 有 $3$ 个包含两个点的集合； - 有 $1$ 个包含四个点的集合。 因此，这个例子中不同非空点集的数量为 $2 + 3 + 0 + 1 = 6$。  由 ChatGPT 4.1 翻译