Dynamic Diameter

## 题目描述 有一个 $n$ 个点的带权无向树，$q$ 次操作，每次修改一条边的权值，要求在每次修改后，输出树的直径大小，强制在线。 ## 输入格式 第一行，$3$ 个由空格分隔的整数 $n,q,w$,（$2\le n\le 10^5$, $1\le q\le 10^5$, $1\le w\le 2\times 10^{13}$），代表有 $n$ 个点，$q$ 次修改，操作过程中每条边的最大权值为 $w-1$。 之后 $n-1$ 行，每行3个整数 $a，b，c$（$1\le a,b\le n$, $0\le c<w$），表示最初树中有一条连接 $a$ 和 $b$，权值为 $c$ 的边。 之后 $q$ 行，每行 $2$ 个整数 $d,e$（$0\le d<n-1$, $0\le e<w$）,你需要通过一定的方法对数据进行解密： - `D=(d+las) mod (n-1)` - `E=(e+las) mod w` 其中 $las$ 为上一次输出的结果（初始 $las=0$），表示将第 $D+1$ 条边的权值改为 $E$。 ## 输出格式 输出 $q$ 行，每行一个整数，表示这次修改后树的直径。 ## 评分标准 子任务1（11分）$n,q\le 100,w\le 10000$ 子任务2（13分）$n,q\le 5000,w\le 10000$ 子任务3（7分）$w\le 10000$,树为以 $1$ 号点为中心的菊花图 子任务4（18分）$w\le 10000$,树为以 $1$ 号点为根的平衡二叉树 子任务5（24分）任意时刻存在一条树的直径经过 $1$ 号点 子任务6（27分）无特殊约定

You are given a weighted undirected tree on $ n $ vertices and a list of $ q $ updates. Each update changes the weight of one edge. The task is to output the diameter of the tree after each update. (The distance between two vertices is the sum of the weights on the unique simple path that connects them. The diameter is the largest of all those distances.)

The first line contains three space-separated integers $ n $ , $ q $ and $ w $ ( $ 2 \leq n \leq 100,000, 1 \leq q \leq 100,000 $ , $ 1 \leq w \leq 20,000,000,000,000 $ ) – the number of vertices in the tree, the number of updates and the limit on the weights of edges. The vertices are numbered $ 1 $ through $ n $ . Next, $ n-1 $ lines describing the initial tree follow. The $ i $ -th of these lines contains three space-separated integers $ a_i $ , $ b_i $ , $ c_i $ ( $ 1 \leq a_i, b_i \leq n $ , $ 0 \leq c_i < w $ ) meaning that initially, there is an edge between vertices $ a_i $ and $ b_i $ with weight $ c_i $ . It is guaranteed that these $ n-1 $ lines describe a tree. Finally, $ q $ lines describing queries follow. The $ j $ -th of these lines contains two space-separated integers $ d_j $ , $ e_j $ ( $ 0 \leq d_j < n - 1, 0 \leq e_j < w $ ). These two integers are then transformed according to the following scheme: - $ d'_j = (d_j + last) \bmod (n - 1) $ - $ e'_j = (e_j + last) \bmod w $ where $ last $ is the result of the last query (initially $ last=0 $ ). Tuple $ (d'_j, e'_j) $ represents a query which takes the $ d'_j+1 $ -th edge from the input and sets its weight to $ e'_j $ .

Output $ q $ lines. For each $ i $ , line $ i $ should contain the diameter of the tree after the $ i $ -th update. Scoring Subtask 1 (11 points): $ n,q \leq 100 $ and $ w \leq 10,000 $ Subtask 2 (13 points): $ n,q \leq 5,000 $ and $ w \leq 10,000 $ Subtask 3 (7 points): $ w \leq 10,000 $ and the edges of the tree are exactly all valid edges of the form $ \{1, i\} $ (Hence, the tree is a star centered at vertex 1.) Subtask 4 (18 points): $ w \leq 10,000 $ , and the edges of the tree are exactly all valid edges of the forms $ \{i, 2i\} $ and $ \{i, 2i+1\} $ (Hence, if we were to root the tree at vertex 1, it would be a balanced binary tree.) Subtask 5 (24 points): it is guaranteed that after each update a longest simple path goes through vertex $ 1 $ Subtask 6 (27 points): no additional constraints

4 3 2000
1 2 100
2 3 1000
2 4 1000
2 1030
1 1020
1 890

2030
2080
2050

10 10 10000
1 9 1241
5 6 1630
10 5 1630
2 6 853
10 1 511
5 3 760
8 3 1076
4 10 1483
7 10 40
8 2051
5 6294
5 4168
7 1861
0 5244
6 5156
3 3001
8 5267
5 3102
8 3623

6164
7812
8385
6737
6738
7205
6641
7062
6581
5155

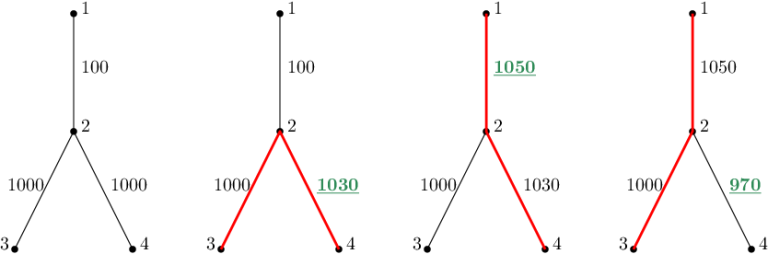
The first sample is depicted in the figure below. The left-most picture shows the initial state of the graph. Each following picture depicts the situation after an update. The weight of the updated edge is painted green, and the diameter is red.  The first query changes the weight of the $ 3 $ rd edge, i.e. $ \{2, 4\} $ , to $ 1030 $ . The largest distance between any pair of vertices is $ 2030 $ – the distance between $ 3 $ and $ 4 $ . As the answer is $ 2030 $ , the second query is $$ d'_2 = (1 + 2030) \bmod 3 = 0 $$ $$ e'_2 = (1020 + 2030) \bmod 2000 = 1050 $$ Hence the weight of the edge $ \{1, 2\} $ is changed to $ 1050 $ . This causes the pair $ \{1, 4\} $ to be the pair with the greatest distance, namely $2080$ . The third query is decoded as $$ d'_3 = (1 + 2080) \bmod 3 = 2 $$ $$ e'_3 = (890 + 2080) \bmod 2000 = 970 $$ As the weight of the edge $ \{2, 4\} $ decreases to $ 970 $ , the most distant pair is suddenly $ \{1, 3\} $ with $2050$ .