CF1194B Yet Another Crosses Problem

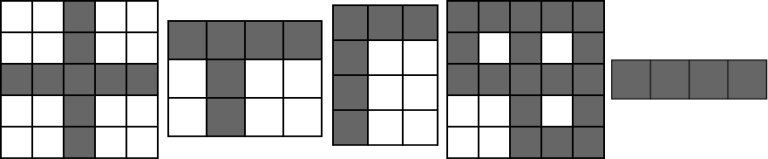
你将会得到若干个 $n$ 行 $m$ 列的矩阵。每一格都被涂成了黑色或白色 若矩阵中的某行，某列都为黑色，则这一行与一列构成了一个十字架 如下所示，这些矩阵都包含了至少一个十字架  而下列矩阵则不包含十字架  你的任务是，共有 $q$ 次询问。对于每一次询问，给出一个矩阵，求出至少还要将多少个白色格子涂成黑色，才能使这个矩阵包含至少一个十字架

第一行包含了一个正整数 $q (1 \leq q \leq 5 \times 10^4)$，意义如上 在每一个询问中，第一行包含了两个正整数 $n, m(1 \leq n, m \leq 5 \times 10^4, n \times m \leq 4 \times 10^5)$，意义如上 接下来会给出 $n$ 行字符，每行 $m$ 个。若第 $i$ 行 $j$ 个字符为 '.'，则代表矩阵的第 $i, j$ 格为白色，'*' 代表黑色 保证 $\displaystyle \sum n \leq 5 \times 10^4$ 且 $\displaystyle \sum n \times m \leq 4 \times 10^5$

输出 $q$ 行，每行包含一个正整数，要求如上

The example contains all the pictures from above in the same order. The first 5 pictures already contain a cross, thus you don't have to paint anything. You can paint $ (1, 3) $ , $ (3, 1) $ , $ (5, 3) $ and $ (3, 5) $ on the $ 6 $ -th picture to get a cross in $ (3, 3) $ . That'll take you $ 4 $ minutes. You can paint $ (1, 2) $ on the $ 7 $ -th picture to get a cross in $ (4, 2) $ . You can paint $ (2, 2) $ on the $ 8 $ -th picture to get a cross in $ (2, 2) $ . You can, for example, paint $ (1, 3) $ , $ (3, 1) $ and $ (3, 3) $ to get a cross in $ (3, 3) $ but that will take you $ 3 $ minutes instead of $ 1 $ . There are 9 possible crosses you can get in minimum time on the $ 9 $ -th picture. One of them is in $ (1, 1) $ : paint $ (1, 2) $ and $ (2, 1) $ .