CF1194E Count The Rectangles

在平面上画有 $n$ 条线段，第 $i$ 条线段连接两点 $(x_{i,1}, y_{i,1})$ 和 $(x_{i,2}, y_{i,2})$。每条线段都是非退化的，并且要么是水平的，要么是竖直的——形式化地说，对于每个 $i \in [1, n]$，要么 $x_{i,1} = x_{i,2}$，要么 $y_{i,1} = y_{i,2}$（但两者不会同时成立）。只有不同类型的线段才可能相交：任意两条水平线段不会有公共点，任意两条竖直线段也不会有公共点。 我们称编号为 $h_1$、$h_2$、$v_1$ 和 $v_2$ 的四条线段（满足 $h_1 < h_2$ 且 $v_1 < v_2$）能够组成一个矩形，当且仅当满足以下条件： - 线段 $h_1$ 和 $h_2$ 是水平线段； - 线段 $v_1$ 和 $v_2$ 是竖直线段； - 线段 $h_1$ 与 $v_1$ 相交； - 线段 $h_2$ 与 $v_1$ 相交； - 线段 $h_1$ 与 $v_2$ 相交； - 线段 $h_2$ 与 $v_2$ 相交。 请计算有多少种选择四条线段的方法，使它们能够组成一个矩形。注意，必须满足 $h_1 < h_2$ 且 $v_1 < v_2$。

第一行包含一个整数 $n$（$1 \le n \le 5000$），表示线段的数量。 接下来 $n$ 行，每行包含四个整数 $x_{i,1}$、$y_{i,1}$、$x_{i,2}$ 和 $y_{i,2}$，表示第 $i$ 条线段的两个端点的坐标。所有端点的坐标范围均为 $[-5000, 5000]$。 保证每条线段都是非退化的，并且要么是水平的，要么是竖直的。此外，如果两条线段有公共点，则其中一条是水平线段，另一条是竖直线段。

输出一个整数，表示能够组成矩形的四条线段的选择方法数。

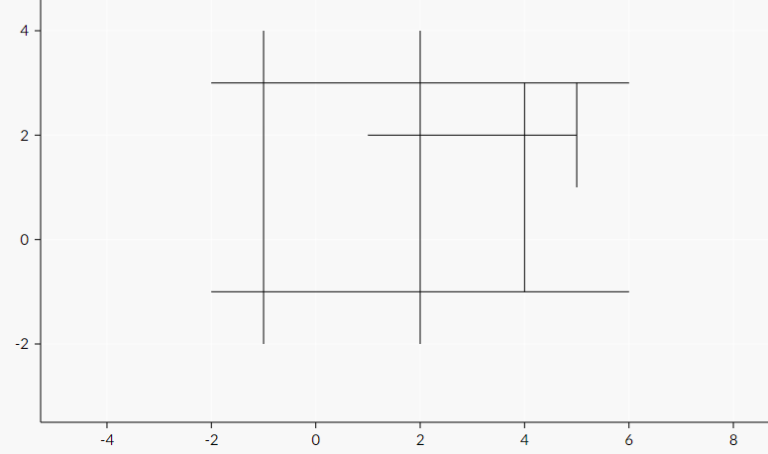
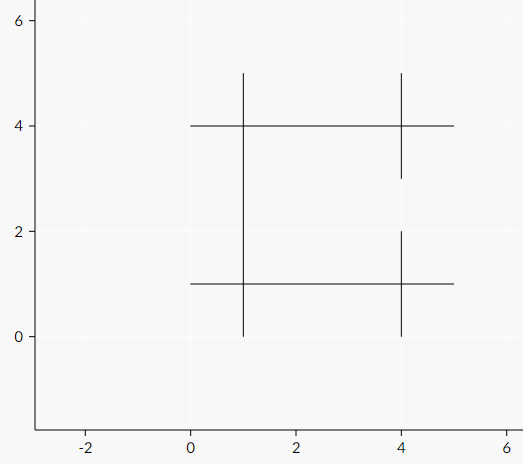
下图展示了样例的情况：   由 ChatGPT 4.1 翻译