CF1195E OpenStreetMap

Seryozha 正在进行一项关于绘制 Stepanovo 度假中心高程图的课程。他在地图上铺设了一个 $n \times m$ 的矩形网格（网格的行从北到南编号为 $1$ 到 $n$，列从西到东编号为 $1$ 到 $m$）。随后，他测量了每个格子相对于 Rybinsk 海平面的平均高度，得到了一个 $n \times m$ 的高程矩阵。第 $(i, j)$ 个格子位于第 $i$ 行与第 $j$ 列的交点，高度为 $h_{i, j}$。 Seryozha 想在浏览器中查看他的工作成果。他的笔记本屏幕一次可以显示高程矩阵中的一个 $a \times b$ 的子矩形（$1 \le a \le n$，$1 \le b \le m$）。Seryozha 想要分析天气对度假中心的影响——例如下雨时，所有雨水会汇聚到哪里。为此，他需要找到屏幕上显示的所有格子中高度最小的那个格子。 请帮助 Seryozha 计算所有可能的屏幕显示子矩形中最小高度的格子的高度之和。换句话说，你需要计算所有大小为 $a \times b$、左上角在 $(i, j)$ 的子矩阵（$1 \le i \le n - a + 1$，$1 \le j \le m - b + 1$）中最小高度的总和。 已知数列 $g_i = (g_{i - 1} \cdot x + y) \bmod z$。给定整数 $g_0$、$x$、$y$ 和 $z$。巧合的是，$h_{i, j} = g_{(i - 1) \cdot m + j - 1}$。

第一行包含四个整数 $n$、$m$、$a$ 和 $b$（$1 \le n, m \le 3000$，$1 \le a \le n$，$1 \le b \le m$），分别表示高程矩阵的行数、列数，以及笔记本屏幕一次能显示的行数和列数。 第二行包含四个整数 $g_0$、$x$、$y$ 和 $z$（$0 \le g_0, x, y < z \le 10^9$）。

输出一个整数，表示所有可能的子矩阵中最小高度的总和。

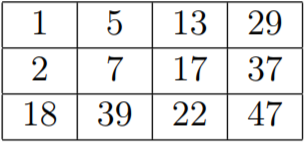
第一个样例中的矩阵如下：  由 ChatGPT 4.1 翻译