CF1197A DIY Wooden Ladder

Let's denote a $ k $ -step ladder as the following structure: exactly $ k + 2 $ wooden planks, of which - two planks of length at least $ k+1 $ — the base of the ladder; - $ k $ planks of length at least $ 1 $ — the steps of the ladder; Note that neither the base planks, nor the steps planks are required to be equal. For example, ladders $ 1 $ and $ 3 $ are correct $ 2 $ -step ladders and ladder $ 2 $ is a correct $ 1 $ -step ladder. On the first picture the lengths of planks are $ [3, 3] $ for the base and $ [1] $ for the step. On the second picture lengths are $ [3, 3] $ for the base and $ [2] $ for the step. On the third picture lengths are $ [3, 4] $ for the base and $ [2, 3] $ for the steps. 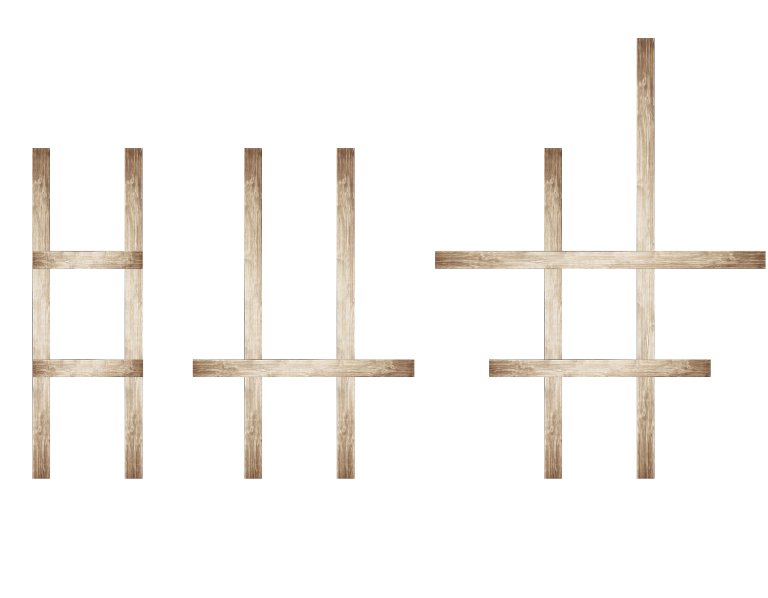You have $ n $ planks. The length of the $ i $ -th planks is $ a_i $ . You don't have a saw, so you can't cut the planks you have. Though you have a hammer and nails, so you can assemble the improvised "ladder" from the planks. The question is: what is the maximum number $ k $ such that you can choose some subset of the given planks and assemble a $ k $ -step ladder using them?

The first line contains a single integer $ T $ ( $ 1 \le T \le 100 $ ) — the number of queries. The queries are independent. Each query consists of two lines. The first line contains a single integer $ n $ ( $ 2 \le n \le 10^5 $ ) — the number of planks you have. The second line contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1 \le a_i \le 10^5 $ ) — the lengths of the corresponding planks. It's guaranteed that the total number of planks from all queries doesn't exceed $ 10^5 $ .

Print $ T $ integers — one per query. The $ i $ -th integer is the maximum number $ k $ , such that you can choose some subset of the planks given in the $ i $ -th query and assemble a $ k $ -step ladder using them. Print $ 0 $ if you can't make even $ 1 $ -step ladder from the given set of planks.

Examples for the queries $ 1-3 $ are shown at the image in the legend section. The Russian meme to express the quality of the ladders: